题目内容
（2011•泉州模拟）圆C的圆心是抛物线x2=4y的焦点，且与抛物线的准线相切，则圆C被y轴截得的弦长是
4
4
．分析：因为所求圆的圆心为抛物线x2=4y的焦点，所以可求出圆心坐标，又因为圆与抛物线的准线相切，故可得到圆方程，从而可求圆C被y轴截得的弦长．
解答：解：∵抛物线x2=4y的焦点坐标为（0，1），准线方程为y=-1，
∴圆心坐标为（0，1），圆的半径为2
∴圆的方程为x2+（y-1）2=4
令x=0，∴y=3或y=-1
∴圆C被y轴截得的弦长是4
故答案为：4
∴圆心坐标为（0，1），圆的半径为2
∴圆的方程为x2+（y-1）2=4
令x=0，∴y=3或y=-1
∴圆C被y轴截得的弦长是4
故答案为：4
点评：本题以抛物线为载体，考查了抛物线的几何性质，考查圆的标准方程，属于基础题．
练习册系列答案
相关题目
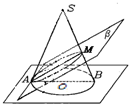（2011•泉州模拟）如图所示，圆锥SO的轴截面△SAB是边长为4的正三角形，M为母线SB的中点，过直线AM作平面β⊥面SAB，设β与圆锥侧面的交线为椭圆C，则椭圆C的短半轴为（ ）