题目内容
在⊙O中,∠A=α,则∠OBC等于( )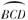
图
A.2α B.90°-α C.180°-2α D.90°+α
解法一:连结OC,则∠BOC=2∠A=2α,
在△OBC中,
∵OB=OC,∴∠OBC=∠OCB.
∴∠OBC=![]() (180°-∠BOC)
(180°-∠BOC)
=![]() (180°-2α)
(180°-2α)
=90°-α.
解法二:延长BO交⊙O于点D,连结CD.
∵∠BCD=90°,∠D=∠A=α,
在Rt△BCD中,
∠OBC=90°-∠D=90°-α.
解法三:延长BO交⊙O于点D,
∵∠BOC=2∠A=2α,
∴∠COD=180°-2α.
∴∠OBC=![]() ∠COD=
∠COD=![]() (180°-2α)
(180°-2α)
=90°-α.
解法四:延长BO到D,连结CD,则![]() 的度数为180°.
的度数为180°.
∵∠A=α,∴![]() 的度数为2α.
的度数为2α.
∴![]() 的度数等于
的度数等于![]() 减去
减去![]() 的度数,
的度数,
即![]() 的度数为180°-2α.
的度数为180°-2α.
又∵∠OBC的度数等于![]() 度数的一半,
度数的一半,
∴∠OBC=![]() (180°-2α)=90°-α.
(180°-2α)=90°-α.
答案:B

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
在⊙O中,弦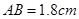 ,圆周角
,圆周角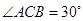 ,则⊙O的直径等于( )
,则⊙O的直径等于( )
A.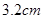 | B.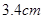 | C.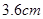 | D.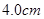 |
 如图,在⊙O中,AB是弦,AC是⊙O的切线,A是切点,过 B作BD⊥AC于D,BD交⊙O于E点,若AE平分
如图,在⊙O中,AB是弦,AC是⊙O的切线,A是切点,过 B作BD⊥AC于D,BD交⊙O于E点,若AE平分