题目内容
18.(1)已知{an}是项数相同的等比数列,求证:{an2}也是等比数列;(2)设数列{an}的前n项和为Sn,若an+Sn=n,cn=an-1,求证:数列{cn}是等比数列.
分析 (1)根据等比数列的定义证明即可.
(2)通过an+Sn=n与an+1+Sn+1=n+1作差、整理可知an+1-1=$\frac{1}{2}$(an-1),进而可知数列{cn}是以-$\frac{1}{2}$为首项、$\frac{1}{2}$为公比的等比数列;
解答 证明:(1){an}是等比数列,设公比为q,当n≥2时,$\frac{{{a}_{n}}^{2}}{{a}_{{n-1}^{2}}}$=($\frac{{a}_{n}}{{a}_{n-1}}$)=q2为常数,故{an2}为等比数列;
(2):∵an+Sn=n,
∴an+1+Sn+1=n+1,
两式相减得:an+1-an+an+1=1,
整理得:an+1-1=$\frac{1}{2}$(an-1),
又∵cn=an-1,
∴cn+1=$\frac{1}{2}$cn,
又∵a1+a1=1,即a1=$\frac{1}{2}$,
∴c1=a1-1=$\frac{1}{2}$-1=-$\frac{1}{2}$,
∴数列{cn}是以-$\frac{1}{2}$为首项、$\frac{1}{2}$为公比的等比数列;
点评 本题考查数列的通项,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
 如图,已知三棱锥A-BCD中,△ABC与△ACD均为边长为2的正三角形,BD=$\sqrt{6}$,证明:面ABC⊥面ACD.
如图,已知三棱锥A-BCD中,△ABC与△ACD均为边长为2的正三角形,BD=$\sqrt{6}$,证明:面ABC⊥面ACD.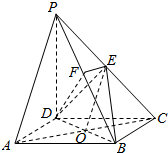 如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点,试通过建立空间直角坐标系解决以下问题:
如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点,试通过建立空间直角坐标系解决以下问题: