Question

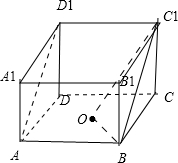
正方体AC₁中，O为底面ABCD中心，则直线AD₁与C₁O所成角大小为

30°

．

Answer 1

分析：由正方体的结构特征，得到AD₁∥BC₁，得到∠OC₁B直线AD₁与C₁O所成角或其补角，通过解△C₁OB求出直线AD₁与C₁O所成角大小．

解答：解：不妨设棱长为1，
因为AD₁∥BC₁，
所以∠OC₁B直线AD₁与C₁O所成角或其补角，
在△C₁OB中，OB=

2

2

，BC1=

2

，OC1=

6

2

，
由余弦定理得到cos∠OC1B=

2+ 3 2 - 1 2

2× 2 × 6 2

=

3

2

所有∠OC₁B=30°
故答案为30°

点评：本题考查的知识点是异面直线及其所成的角，其中根据正方体的几何特征，构造出异面直线AD₁与C₁O所成角∠OC₁B是解答本题的关键．