题目内容
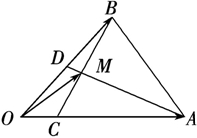如下图所示，在△ABO中，| OC |
| 1 |
| 4 |
| OA |
| OD |
| 1 |
| 2 |
| OB |
| OA |
| a |
| OB |
| b |
| a |
| b |
| OM |
分析：由D，M，A三点共线，可得存在实数m使得
=m
+(1-m)
=(1-m)
+
，同理可得，
=n
+(1-n)
=
+n
，根据向量相等的条件可求m，n，的值，从而可用向量
，
表示
| OM |
| OD |
| OA |
| a |
| m |
| 2 |
| b |
| OM |
| OB |
| OC |
| 1-n |
| 4 |
| a |
| b |
| a |
| b |
| OM |
解答：解：∵D，M，A三点共线，
∴存在实数m使得
=m
+(1-m)
=(1-m)
+
；
又B，M，C三点共线，同理可得，
=n
+(1-n)
=
+n
∴
得m=
∴
=
+
∴存在实数m使得
| OM |
| OD |
| OA |
| a |
| m |
| 2 |
| b |
又B，M，C三点共线，同理可得，
| OM |
| OB |
| OC |
| 1-n |
| 4 |
| a |
| b |
∴
|
| 6 |
| 7 |
∴
| OM |
| 1 |
| 7 |
| a |
| 3 |
| 7 |
| b |
点评：本题主要考查了共线向量的基本定理：若点P在直线AB上，O为直线AB外任意一点，则存在实数λ使得
=λ
+(1-λ)
的应用，属于基础知识的应用．
| OP |
| OA |
| OB |
练习册系列答案
相关题目
=15,连CF并延长交AB于E，则
=_______．
（a1+a2+…+an）的值.