Question

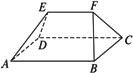
如下图所示，在边长为l的等边△ABC中，⊙O₁为△ABC中内切圆，⊙O₂与⊙O₁外切，且与AB、BC相切，…，⊙O_n+1与⊙O_n外切，且与AB、BC相切，如此无限继续下去，记⊙O_n的面积为a_n（n∈N^*）.

（1）证明{a_n}是等比数列；

（2）求（a₁+a₂+…+a_n）的值.

Answer 1

分析:与几何图形有关的应用问题，首先结合图形分析相邻图形的依赖关系，论证所求问题是否组成一个等比数列且公比的绝对值小于1，然后计算.

解:（1）记r_n为圆O_n的半径，则r₁=tan30°=l，

=sin30°=,

所以r_n=r_n-1（n≥2）.

于是a₁=πr₁²=,

=（）²=,

故{a_n}成等比数列.

（2）因为a_n=（）^n-1a₁（n∈N^*）,

所以（a₁+a₂+…+a_n）

==.