题目内容
若P是等边三角形ABC所在平面外一点,PA=PB=PC=
,△ABC的边长为1,则PC和平面ABC所成的角是( )
| 2 |
| 3 |
分析:取AB中点D,连接PD、CD,可证明出平面PCD⊥平面ABC,从而得到∠PCD是直线PC和平面ABC所成的角.在△PCD中,算出PD、CD的长,用余弦定理算出cos∠PCD的值,从而得到∠PCD的度数,即为PC和平面ABC所成的角.
解答: 解:取AB中点D,连接PD、CD,
解:取AB中点D,连接PD、CD,
∵PA=PB,D为AB中点,∴PD⊥AB,同理可得CD⊥AB
∵PD、CD是平面PCD内的相交直线
∴AB⊥平面PCD
∵AB?平面ABC,∴平面PCD⊥平面ABC,
由此可得直线PC在平面ABC内的射影是直线CD,
∴∠PCD是直线PC和平面ABC所成的角
∵△PAB中,PA=PB=
,AB=1
∴PD=
=
又∵正△ABC中,CD=
AB=
∴△PCD中,cos∠PCD=
=
结合∠PCD是小于180°的正角,可得∠PCD=30°
即PC和平面ABC所成的角等于30°
故选:A
 解:取AB中点D,连接PD、CD,
解:取AB中点D,连接PD、CD,∵PA=PB,D为AB中点,∴PD⊥AB,同理可得CD⊥AB
∵PD、CD是平面PCD内的相交直线
∴AB⊥平面PCD
∵AB?平面ABC,∴平面PCD⊥平面ABC,
由此可得直线PC在平面ABC内的射影是直线CD,
∴∠PCD是直线PC和平面ABC所成的角
∵△PAB中,PA=PB=
| 2 |
| 3 |
∴PD=
PA2-(
|
| ||
| 6 |
又∵正△ABC中,CD=
| ||
| 2 |
| ||
| 2 |
∴△PCD中,cos∠PCD=
| PC2+CD2-PD2 |
| 2PC×CD |
| ||
| 2 |
结合∠PCD是小于180°的正角,可得∠PCD=30°
即PC和平面ABC所成的角等于30°
故选:A
点评:本题在正三棱锥中求侧棱与底面所成角的大小,着重考查了线面垂直、面面垂直的证明和直线与平面所成角大小的求法等知识,属于中档题.

练习册系列答案
相关题目
 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.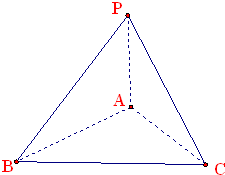 三棱锥P-ABC中,三角形PAB是等边三角形,∠PAC=∠PBC=90°
三棱锥P-ABC中,三角形PAB是等边三角形,∠PAC=∠PBC=90° 如图,三棱锥P-ABC中,PA⊥平面ABC,△ABC是等边三角形,E是BC中点,若PA=AB,则异面直线PE与AB所成角的余弦值( )
如图,三棱锥P-ABC中,PA⊥平面ABC,△ABC是等边三角形,E是BC中点,若PA=AB,则异面直线PE与AB所成角的余弦值( ) 如图,在三棱锥P-ABC中,△PAB是等边三角形,D,E分别为AB,PC的中点.
如图,在三棱锥P-ABC中,△PAB是等边三角形,D,E分别为AB,PC的中点.