题目内容
直角坐标平面中,过点A1(1,0)作函数f(x)=x2(x>0)的切线l1,其切点为B1(x1,y1);过点A2(x1,0)作函数g(x)=ex(x>0)的切线l2,其切点为B2(x2,y2);过点A3(x2,0)作函数f(x)=x2(x>0)的切线l3,其切点为B3(x3,y3);如此下去,即过点A2k-2(x2k-2,0)作函数f(x)=x2(x>0)的切线l2k-1,其切点为B2k-1(x2k-1,y2k-1);过点A2k-1(x2k-1,0)作函数g(x)=ex(x>0)的切线l2k,其切点为B2k(x2k,y2k);….(1)求x2k-2与x2k-1及x2k-1与x2k的关系;
(2)求数列{xn}通项公式xn;
(3)是否存在实数t,使得对于任意的自然数n,不等式
| 1 |
| x2+1 |
| 2 |
| x4+1 |
| 3 |
| x6+1 |
| n |
| x2n+1 |
| 6 |
| t |
分析:(1)可利用导数几何意义求出以B2k-1(x2k-1,y2k-1)为切点的切线l2k-1的方程,又因为切线l2k-1过点A2k-2(x2k-2,0),代入可得x2k-2与x2k-1的关系;同理可得x2k-1与x2k的关系;
(2)由(1)的递推关系可得x2k=2x2k-2+1,用构造新数列法,可知数列{x2k+1}为等比数列,从而求得此数列的通项公式,进而求得{x2k}的通项公式,再利用x2k-2与x2k-1的关系,求出数列{x2k-1}的通项公式,最后写出数列
{xn}通项公式即可
(3)利用错位相减法将Sn=
+
+
+…+
+1求和,再利用Sn+1-Sn>0证明其为递增数列,所以将Sn的最大值是
Sn,利用数列极限的求法可求出此值,再使t-
不小于这个极限值,解不等式得t的取值范围
(2)由(1)的递推关系可得x2k=2x2k-2+1,用构造新数列法,可知数列{x2k+1}为等比数列,从而求得此数列的通项公式,进而求得{x2k}的通项公式,再利用x2k-2与x2k-1的关系,求出数列{x2k-1}的通项公式,最后写出数列
{xn}通项公式即可
(3)利用错位相减法将Sn=
| 1 |
| x2+1 |
| 2 |
| x4+1 |
| 3 |
| x6+1 |
| n |
| x2n+1 |
| lim |
| n→∞ |
| 6 |
| t |
解答:解:(1)∵f′(x)=2x,
∴切线l2k-1的方程为y-x2k-12=2x2k-1(x-x2k-1),又切线l2k-1过点A2k-2(x2k-2,0),
∴0-x2k-12=2x2k-1(x2k-2-x2k-1),且x2k-1>0,
∴x2k-1=2x2k-2.
∴x1=2.
又∵g′(x)=(ex)′=ex,
∴切线l2k的方程为y-ex2k=ex2k(x-x2k),而切线l2k过点A2k-1(x2k-1,0),
∴0-ex2k=ex2k(x2k-1-x2k),且x2k>0,
∴x2k=x2k-1+1.
∴x2=x1+1=3.
故x2k-2与x2k-1的关系为x2k-1=2x2k-2; x2k-1与x2k的关系为x2k=x2k-1+1.
(2)由(1)可知x2k=x2k-1+1=2x2k-2+1,即x2k+1=2(x2k-2+1),
∴数列{x2k+1}为等比数列,且首项为4,
∴x2k+1=4×2k-1,即x2k=2k+1-1.
而x2k-1=2x2k-2=2(2k-1)=2k+1-2,故数列{xn}通项公式为xn=
(3)(理)令Sn=
+
+
+…+
+1=
+
+
+…+
,
∴
Sn=
+
+
+…+
,
两式相减得
Sn=
+
+
+
+…+
-
=
-
=
(1-
)-
,
∴Sn=1-
-
=1-
.
∴Sn+1-Sn=(1-
)-(1-
)=
>0,
∴数列{Sn}递增.
又当n≥6时,2n+1=2(1+1)n=2(1+Cn1+Cn2+Cn1+CCn3+…+Cnn-3+Cnn-2+Cnn-1+Cnn)>4(1+Cn1+Cn2)>2(n2+n),
∴0<
<
,而
=0,
∴
Sn=1.
∴对于任意的自然数n不等式恒成立等价于t-
≥1,
∴t[-2,0)∪[3,+∞)
∴切线l2k-1的方程为y-x2k-12=2x2k-1(x-x2k-1),又切线l2k-1过点A2k-2(x2k-2,0),
∴0-x2k-12=2x2k-1(x2k-2-x2k-1),且x2k-1>0,
∴x2k-1=2x2k-2.
∴x1=2.
又∵g′(x)=(ex)′=ex,
∴切线l2k的方程为y-ex2k=ex2k(x-x2k),而切线l2k过点A2k-1(x2k-1,0),
∴0-ex2k=ex2k(x2k-1-x2k),且x2k>0,
∴x2k=x2k-1+1.
∴x2=x1+1=3.
故x2k-2与x2k-1的关系为x2k-1=2x2k-2; x2k-1与x2k的关系为x2k=x2k-1+1.
(2)由(1)可知x2k=x2k-1+1=2x2k-2+1,即x2k+1=2(x2k-2+1),
∴数列{x2k+1}为等比数列,且首项为4,
∴x2k+1=4×2k-1,即x2k=2k+1-1.
而x2k-1=2x2k-2=2(2k-1)=2k+1-2,故数列{xn}通项公式为xn=
|
(3)(理)令Sn=
| 1 |
| x2+1 |
| 2 |
| x4+1 |
| 3 |
| x6+1 |
| n |
| x2n+1 |
| 1 |
| 22 |
| 2 |
| 23 |
| 3 |
| 24 |
| n |
| 2n+1 |
∴
| 1 |
| 2 |
| 1 |
| 23 |
| 2 |
| 24 |
| 3 |
| 25 |
| n |
| 2n+2 |
两式相减得
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 2 |
| 24 |
| 3 |
| 25 |
| n |
| 2n+1 |
| n |
| 2n+2 |
=
| ||||
1-
|
| n |
| 2n+2 |
| 1 |
| 2 |
| 1 |
| 2n |
| n |
| 2n+2 |
∴Sn=1-
| 1 |
| 2n |
| n |
| 2n+1 |
| n+2 |
| 2n+1 |
∴Sn+1-Sn=(1-
| n+3 |
| 2n+2 |
| n+2 |
| 2n+1 |
| n+1 |
| 2n+2 |
∴数列{Sn}递增.
又当n≥6时,2n+1=2(1+1)n=2(1+Cn1+Cn2+Cn1+CCn3+…+Cnn-3+Cnn-2+Cnn-1+Cnn)>4(1+Cn1+Cn2)>2(n2+n),
∴0<
| n+1 |
| 2n+1 |
| n+2 |
| 2(n2+n) |
| lim |
| n→∞ |
| n+2 |
| 2(n2+n) |
∴
| lim |
| n→∞ |
∴对于任意的自然数n不等式恒成立等价于t-
| 6 |
| t |
∴t[-2,0)∪[3,+∞)
点评:本题综合考查了利用递推公式求通项公式,错位相减求和,数列最值的求法,特别是与函数的结合,使本题的综合性提高,解决本题需要扎实的基本功.

练习册系列答案
相关题目
 +
+ +
+ +…+
+…+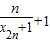 ≤t-
≤t- 恒成立?若存在,求出这样的实数t的取值范围;若不存在,则说明理由.
恒成立?若存在,求出这样的实数t的取值范围;若不存在,则说明理由.