题目内容
(本小题满分12分) 已知 为等比数列,其中
为等比数列,其中 ,且
,且 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)首先根据条件可得 ,再由等比数列
,再由等比数列 可得
可得 ,从而
,从而 ,因此数列
,因此数列 的通项公式为
的通项公式为 ;(2)由(1)可得
;(2)由(1)可得 ,这是一个等比数列与一个等差数列的乘积,因此可以考虑用错位相减法来求数列
,这是一个等比数列与一个等差数列的乘积,因此可以考虑用错位相减法来求数列 的前
的前 项和:
项和:
 ,
,
 ,
,

 ,
,
 .
.
试题解析:(1)∵ 成等差数列,∴
成等差数列,∴ ,
,
又∵等比数列 ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ,
,
∴数列 的通项公式为
的通项公式为 ;
;
(2)∵ ,∴
,∴ ,
,
∵ ,
,
∴
 ,
,
∴ .
.
考点:1.等差等比数列的通项公式与性质;2.错位相减法求数列的和.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 (i为虚数单位),则z等于( )
(i为虚数单位),则z等于( ) B.-l+2i C.l-3i D.l-2i
B.-l+2i C.l-3i D.l-2i 的展开式中,
的展开式中, 的系数为( )
的系数为( )  (B)
(B) (C)
(C) (D)
(D)
 ,
, 的运算原理如图所示,设
的运算原理如图所示,设 ,
, ,则输出的
,则输出的 的最大值与最小值的差为( )
的最大值与最小值的差为( )
 B.
B. C.
C. D.
D.
 ,
, 且
且 .
. 在点
在点 处的切线垂直于
处的切线垂直于 轴,求实数
轴,求实数 的值;
的值; 时,求函数
时,求函数 的最小值;
的最小值; 与
与 的图像存在三个交点,求
的图像存在三个交点,求 的取值范围.
的取值范围. 的展开式中第四项的系数为 .
的展开式中第四项的系数为 . 中,已知
中,已知 ,
, ,则使得
,则使得 的最小正整数
的最小正整数 为( )
为( ) B.
B. C.
C. D.
D.
 ,函数
,函数 ,则
,则 的值等于( )
的值等于( ) B.
B. C.
C. D.
D.
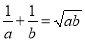 ,且
,且 ,求
,求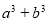 的最小值.
的最小值.