题目内容
已知向量
=(sinx,
),
=(sinx+
cosx,3),f(x)=
•
△ABC三个内角A,B,C的对边分别为a,b,c,且f(A)=3.
(1)求角A的大小;
(2)若a=
,b=1,求c的值.
| m |
| 1 |
| 2 |
| n |
| 3 |
| m |
| n |
(1)求角A的大小;
(2)若a=
| 3 |
考点:余弦定理,平面向量数量积的运算,正弦定理
专题:解三角形,平面向量及应用
分析:(1)由平面向量数量积的运算可得解析式f(x)=sin(2x-
)+2,由已知可得sin(2A-
)=1,由2A-
∈(-
,
),可解得A的值.
(2)法一:由余弦定理可得c2-c-2=0,即可解得c的值;法二:由正弦定理可得sinB=
,又b<a,即可求B,从而求C及c的值.
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 11π |
| 6 |
(2)法一:由余弦定理可得c2-c-2=0,即可解得c的值;法二:由正弦定理可得sinB=
| 1 |
| 2 |
解答:
解:(1)因为f(x)=
•
=sin2x+
sinxcosx+
=
+
+
=sin(2x-
)+2…4分
所以f(A)=sin(2A-
)+2=3,即sin(2A-
)=1,
因为2A-
∈(-
,
),
所以2A-
=
,所以A=
.…8分
(2)法一:由余弦定理a2=b2+c2-2bccosA,
可得c2-c-2=0,所以c=2或c=-1(舍去).…10分
法二:由正弦定理
=
,可得sinB=
,又b<a,所以B=
,
所以C=
,所以c=2…12分
| m |
| n |
| 3 |
| 3 |
| 2 |
=
| 1-cos2x |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
=sin(2x-
| π |
| 6 |
所以f(A)=sin(2A-
| π |
| 6 |
| π |
| 6 |
因为2A-
| π |
| 6 |
| π |
| 6 |
| 11π |
| 6 |
所以2A-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
(2)法一:由余弦定理a2=b2+c2-2bccosA,
可得c2-c-2=0,所以c=2或c=-1(舍去).…10分
法二:由正弦定理
| a |
| sinA |
| b |
| sinB |
| 1 |
| 2 |
| π |
| 6 |
所以C=
| π |
| 2 |
点评:本题主要考查平面向量数量积的运算,余弦定理,正弦定理的应用,属于基本知识的考查.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
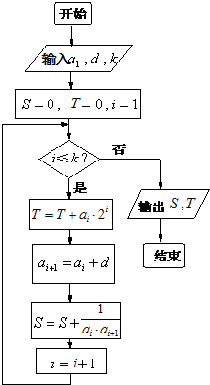 如图所示,程序框图给出了无穷正项数列{an}满足的条件,且当k=5时,输出的S是
如图所示,程序框图给出了无穷正项数列{an}满足的条件,且当k=5时,输出的S是 设y=f(x)为定义在R上的偶函数,当x≤-1时,y=f(x)的图象是经过点(-2,2),斜率为-1的一条射线,又当x∈[-1,0]时,y=f(x)的图象是顶点在(0,2),且过点(-1,1)的一段抛物线.
设y=f(x)为定义在R上的偶函数,当x≤-1时,y=f(x)的图象是经过点(-2,2),斜率为-1的一条射线,又当x∈[-1,0]时,y=f(x)的图象是顶点在(0,2),且过点(-1,1)的一段抛物线.