题目内容
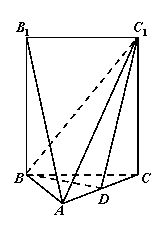
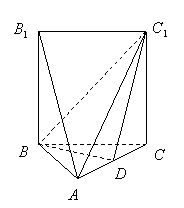
如图,五面体![]() 中,
中,![]() .底面
.底面![]() 是正三角形,
是正三角形,![]() .四边形
.四边形![]() 是矩形,二面角
是矩形,二面角![]() 为直二面角.
为直二面角.
(Ⅰ)若![]() 是
是![]() 中点,求证:
中点,求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求该五面体的体积.
 |
解:(Ⅰ)证明:连结![]() 交
交![]() 于
于![]() ,连结
,连结![]()
∵ 四边形![]() 是矩形 ∴
是矩形 ∴![]() 为
为![]() 中点又
中点又![]() 为
为![]() 中点,
中点,
从而![]() (4分)∵
(4分)∵![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() (6分)
(6分)
 |
(Ⅱ)过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() 为正三角形,
为正三角形,
![]() 为
为![]() 中点,
中点,![]() (8分)
(8分)
![]() 二面角
二面角![]() 为直二面角,
为直二面角,![]() 面
面![]() ,又
,又![]() ,故矩形
,故矩形![]() 的面积
的面积![]() (10分)
(10分)
故所求五面体体积![]() (12分)
(12分)

练习册系列答案
相关题目
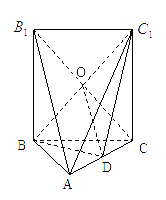
 中,
中,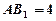 .底面
.底面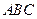 是正三角形,
是正三角形,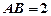 .四边形
.四边形 是矩形,二面角
是矩形,二面角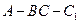 为直二面角.
为直二面角.
 在
在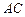 上运动,当
上运动,当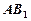 ∥平面
∥平面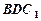 ,
, 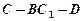 余弦值.
余弦值.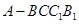 中,
中,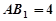 .底面
.底面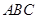 是正三角形,
是正三角形,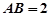 .四边形
.四边形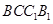 是矩形,二面角
是矩形,二面角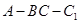 为直二面角.
为直二面角.
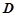 在
在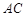 上运动,当
上运动,当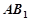 ∥平面
∥平面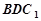 ,
,  余弦值.
余弦值.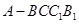 中,
中,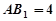 .底面
.底面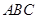 是正三角
是正三角 .四边形
.四边形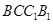 是矩形,二面角
是矩形,二面角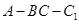 为
为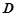 在
在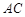 上运动,当
上运动,当 ∥平面
∥平面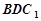 ,
,
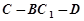 余弦值.
余弦值.
 如图,五面体
如图,五面体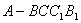 中,
中,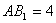 .底面
.底面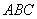 是正三角形,
是正三角形,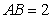 .四边形
.四边形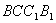 是矩形,平面
是矩形,平面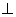 平面
平面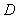 在
在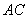 上运动,问:当
上运动,问:当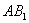 ∥平面
∥平面 ,请说明理由;
,请说明理由; 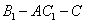 的余弦值.
的余弦值.