题目内容

在△ABC中，AD是BC边上的中线，且AC=2AB=2AD=4，则BD=________．

$\text{[math]}$
分析：依题意， $\text{[math]}$ = $\text{[math]}$ （ $\text{[math]}$ + $\text{[math]}$ ），等号两端平方，利用余弦定理可求得BC的长，从而可得答案．
解答：在△ABC中，∵AD是BC边上的中线，
∴ $\text{[math]}$ = $\text{[math]}$ （ $\text{[math]}$ + $\text{[math]}$ ），等号两端平方，
$\text{[math]}$ = $\text{[math]}$ （ $\text{[math]}$ + $\text{[math]}$ +2| $\text{[math]}$ |•| $\text{[math]}$ |cosA）
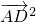即2²= $\text{[math]}$ （2²+4²+2×2×4cosA），
∴cosA=- $\text{[math]}$ ，
∴有余弦定理得：|BC|²=a²=b²+c²-2bccosA
=4+16-2×2×4×（- $\text{[math]}$ ）
=24，
∴a=2 $\text{[math]}$ ，
∴|BD|= $\text{[math]}$ |BC|= $\text{[math]}$ a= $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：本题考查向量间的位置关系，考查向量的模与向量的数量积及余弦定理，属于中档题．

练习册系列答案

初中生学业评价指导用书系列答案

阅读计划初中课外现代文拓展阅读系列答案

伴你学习新课程单元过关练习系列答案

中考综合学习评价与检测系列答案

新课程初中学习能力自测丛书系列答案

初中毕业升学考试指导系列答案

学生课程精巧训练系列答案

名师点睛学练考系列答案

南大励学小学生英语四合一阅读组合训练系列答案

学业测评课时练测加全程测控系列答案

相关题目

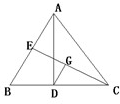选做题（请考生在以下三个小题中任选一题作答，如果多做，则按所做的第一题评阅记分）
A．（选修4-4坐标系与参数方程）将参数方程

（e为参数）化为普通方程是

．
B．（选修4-5 不等式选讲）不等式|x-1|+|2x+3|＞5的解集是

．
C．（选修4-1 几何证明选讲）如图，在△ABC中，AD是高线，CE是中线，|DC|=|BE|，DG⊥CE于G，且|EC|=8，则|EG|=

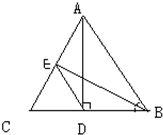在△ABC中，AD是BC边上的高，垂足为D点．BE是∠ABC的角平分线，并交AC于E点．若BC=6，CA=7，AB=8．
（1）求DE的长；
（2）求△ABC的面积．

在△ABC中，AD是BC边上的中线，且AC=2AB=2AD=4，则BD=

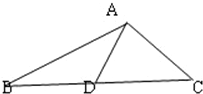如图，在△ABC中，AD是BC边上的中线，AB=5，AC=3，AD=2，求：BC的长及面积S_△ABC．

如下图所示，在△ABC中，AD是BC边上的中线，F是AD上的一点，且=15,连CF并延长交AB于E，则=_______．