题目内容
已知椭圆E的对称轴为坐标轴,焦点在y轴上,离心率 ,A,B分别为椭圆的上顶点和右顶点,且
,A,B分别为椭圆的上顶点和右顶点,且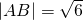 .
.
(1)求椭圆E的方程;
(2)已知直线l:y=x+m与椭圆E相交于M,N两点,且OM⊥ON(其中O为坐标原点),求m的值.
解:(1)设椭圆的方程为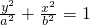 (a>b>0),半焦距为c,
(a>b>0),半焦距为c,
由 得,
得,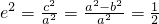 ,得a2=2b2…(2分)
,得a2=2b2…(2分)
由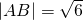 得,a2+b2=6,…(4分)
得,a2+b2=6,…(4分)
故a2=4,b2=2
所以,椭圆E的方程为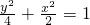 …(6分)
…(6分)
(2)由 ,消去y,并整理得:3x2+2mx+m2-4=0,…(7分)
,消去y,并整理得:3x2+2mx+m2-4=0,…(7分)
由判别式△=4m2-12(m2-4)>0,解得 …(9分)
…(9分)
设M(x1,y1),N(x2,y2),则 ,
, …(10分)
…(10分)
由OM⊥ON,得 …(11分)
…(11分)
又 =
= ,
,
故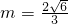 …(14分)
…(14分)
分析:(1)利用待定系数法,根据离心率 ,且
,且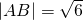 ,建立方程,求得几何量,即可求椭圆E的方程;
,建立方程,求得几何量,即可求椭圆E的方程;
(2)直线方程代入椭圆方程,利用韦达定理及OM⊥ON,建立方程,可求m的值.
点评:本题考查椭圆的标准方程,考查椭圆的几何性质,考查直线与椭圆的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.
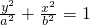 (a>b>0),半焦距为c,
(a>b>0),半焦距为c,由
 得,
得,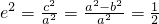 ,得a2=2b2…(2分)
,得a2=2b2…(2分)由
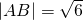 得,a2+b2=6,…(4分)
得,a2+b2=6,…(4分)故a2=4,b2=2
所以,椭圆E的方程为
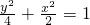 …(6分)
…(6分)(2)由
 ,消去y,并整理得:3x2+2mx+m2-4=0,…(7分)
,消去y,并整理得:3x2+2mx+m2-4=0,…(7分)由判别式△=4m2-12(m2-4)>0,解得
 …(9分)
…(9分)设M(x1,y1),N(x2,y2),则
 ,
, …(10分)
…(10分)由OM⊥ON,得
 …(11分)
…(11分)又
 =
= ,
,故
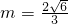 …(14分)
…(14分)分析:(1)利用待定系数法,根据离心率
 ,且
,且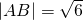 ,建立方程,求得几何量,即可求椭圆E的方程;
,建立方程,求得几何量,即可求椭圆E的方程;(2)直线方程代入椭圆方程,利用韦达定理及OM⊥ON,建立方程,可求m的值.
点评:本题考查椭圆的标准方程,考查椭圆的几何性质,考查直线与椭圆的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,A,B分别为椭圆的上顶点和右顶点,且
,A,B分别为椭圆的上顶点和右顶点,且 .
. ,A,B分别为椭圆的上顶点和右顶点,且
,A,B分别为椭圆的上顶点和右顶点,且 .
.