题目内容
如图,在底面为直角梯形的四棱锥 中
中 ,
, 平面
平面 ,
, ,
, ,
, .
.

⑴求证:
 ;
;
(2)设点 在棱
在棱 上,
上, ,若
,若 ∥平面
∥平面 ,求
,求 的值.
的值.
 中
中 ,
, 平面
平面 ,
, ,
, ,
, .
.
⑴求证:

 ;
;(2)设点
 在棱
在棱 上,
上, ,若
,若 ∥平面
∥平面 ,求
,求 的值.
的值.(1)证明略;(2)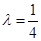 。
。
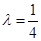 。
。试题分析:(1)∵∠DAB=90°,AD=1,AB=
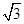 ,∴BD=2,∠ABD=30°,
,∴BD=2,∠ABD=30°,∵BC∥AD∴∠DBC=60°,BC=4,由余弦定理得DC=2
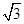 ,
,BC2=DB2+DC2,∴BD⊥DC,
∵PD⊥面ABCD,∴BD⊥PD,PD∩CD=D,∴BD⊥面PDC,
∵PC在面PDC内,∴BD⊥PC。
(2)在底面ABCD内过D作直线DF∥AB,交BC于F,
分别以DA、DF、DP为x、y、z轴建立如图空间坐标系,
A(1,0,0),B(1,
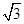 ,0),P(0,0,a)C、(-3,
,0),P(0,0,a)C、(-3,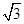 ,0),
,0),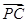 =(-3,
=(-3,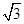 ,-a),
,-a),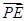 =(-3λ,
=(-3λ,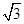 λ,-aλ),
λ,-aλ),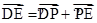 =(0,0,a)+(-3λ,
=(0,0,a)+(-3λ,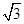 λ,-aλ)=(-3λ,
λ,-aλ)=(-3λ,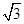 λ,a-aλ),
λ,a-aλ), =(0,
=(0,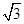 ,0),
,0),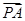 =(1,0,-a),
=(1,0,-a),设
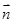 =(x,y,z)为面PAB的法向量,由
=(x,y,z)为面PAB的法向量,由 ·
·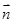 =0,
=0,得y=0,由
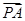 ·
·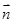 =0,得x-az=0,取x=a,z=1,
=0,得x-az=0,取x=a,z=1,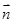 =(a,0,1),
=(a,0,1),由DE∥面PAB得:
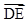 ⊥
⊥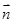
,∴
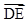 ·
·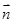 =0,-3aλ+a-aλ=0,∴λ=
=0,-3aλ+a-aλ=0,∴λ=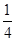 。
。点评:中档题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,(2)利用空间向量,省去繁琐的证明,也是解决立体几何问题的一个基本思路。对计算能力要求较高。

练习册系列答案
相关题目
 ,下半部分是长方体
,下半部分是长方体 。图2、图3分别是该标识墩的正(主)视图和俯视图。
。图2、图3分别是该标识墩的正(主)视图和俯视图。



 的金属球熔成一个圆锥,使圆锥的侧面积为底面积的3倍,则这个圆锥的高为__________.
的金属球熔成一个圆锥,使圆锥的侧面积为底面积的3倍,则这个圆锥的高为__________.


 轴上有一条单位长度的线段
轴上有一条单位长度的线段 ,沿着与其垂直的
,沿着与其垂直的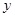 轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形
轴方向平移一个单位长度,线段扫过的区域形成一个二维方体(正方形 ),再把正方形沿着与其所在的平面垂直的
),再把正方形沿着与其所在的平面垂直的 轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体
轴方向平移一个单位长度,则正方形扫过的区域形成一个三维方体(正方体 )。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有
)。请你设想存在四维空间,将正方体向第四个维度平移得到四维方体,若一个四维方体有 个顶点,
个顶点, 条棱,
条棱, 个面,则
个面,则 的值分别为 ( )
的值分别为 ( )






