Question

【题目】已知，函数，.

（1）若在上单调递增，求正数的最大值；

（2）若函数在内恰有一个零点，求的取值范围.

Answer 1

【答案】（1）（2）

【解析】

（1）求出的单调递增区间，令，得，可知区间，即可求出正数的最大值；（2）令，当时，，可将问题转化为在的零点问题，分类讨论即可求出答案.

解：（1）由，

得，.

因为在上单调递增，

令，得时单调递增，

所以解得，可得正数的最大值为.

（2），

设，当时，.它的图形如图所示.

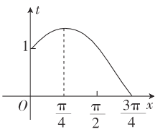
又，则，，令，

则函数在内恰有一个零点，可知在内最多一个零点.

①当0为的零点时，显然不成立；

②当为的零点时，由，得，把代入中，

得，解得，，不符合题意.

③当零点在区间时，若，得，此时零点为1，即，由的图象可知不符合题意；

若，即，设的两根分别为，，由，且抛物线的对称轴为，则两根同时为正，要使在内恰有一个零点，则一个根在内，另一个根在内，

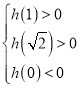所以解得.

综上，的取值范围为.