题目内容
设点P在曲线y=x2+2上,点Q在曲线y=
上,则|PQ|的最小值等于______.
| x-2 |
由y=x2+2,得:x2=y-2,x=±
.
所以,y=x2+2(x≥0)与y=
互为反函数.
它们的图象关于y=x对称.
P在曲线y=x2+2上,点Q在曲线y=
上,
设P(x,x2),Q(x,
)
要使|PQ|的距离最小,则P应在y=x2+2(x≥0)上,
又P,Q的距离为P或Q中一个点到y=x的最短距离的两倍.
以Q点为例,Q点到直线y=x的最短距离
d=
=
=
.
所以dmin=
=
.
则|PQ|的最小值等于2×
=
.
故答案为
.
| y-2 |
所以,y=x2+2(x≥0)与y=
| x-2 |
它们的图象关于y=x对称.
P在曲线y=x2+2上,点Q在曲线y=
| x-2 |
设P(x,x2),Q(x,
| x-2 |
要使|PQ|的距离最小,则P应在y=x2+2(x≥0)上,
又P,Q的距离为P或Q中一个点到y=x的最短距离的两倍.
以Q点为例,Q点到直线y=x的最短距离
d=
|x-
| ||
|
|
| ||||
|
|(
| ||||||
|
所以dmin=
| ||
|
7
| ||
| 8 |
则|PQ|的最小值等于2×
7
| ||
| 8 |
7
| ||
| 4 |
故答案为
7
| ||
| 4 |

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
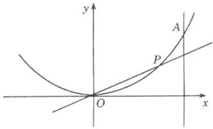 设点P在曲线y=x2上,从原点向A(2,4)移动,如果直线OP,曲线y=x2及直线x=2所围成的面积分别记为S1、S2.
设点P在曲线y=x2上,从原点向A(2,4)移动,如果直线OP,曲线y=x2及直线x=2所围成的面积分别记为S1、S2.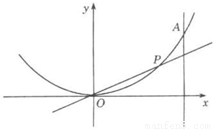
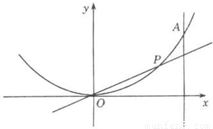
 上,则|PQ|的最小值等于 .
上,则|PQ|的最小值等于 .