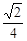在正三棱柱中.若AB=2,=1,则点A到平面的距离为A．B．C．D．题目和参考答案——青夏教育精英家教网—

题目内容

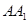在正三棱柱中，若AB=2,=1,则点A到平面的距离为（）

A．

B．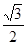

C．

D．

解析试题分析：设点A到平面A1BC的距离为h，则三棱锥的体积为即,∴，∴h=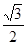
考点：本题考查了空间中点到平面的距离
点评：求点到平面的距离，可以转化为三棱锥底面上的高，用体积相等法，容易求得．“等积法”是常用的求点到平面的距离的方法

练习册系列答案

相关题目

在一个几何体的三视图中，正视图和俯视图如下图所示，则该几何体的体积为（　　　）

cm³

cm³

cm³

设是三个不重合的平面，l是直线，给出下列命题：
①若，则； ②若
③若l上存在两点到的距离相等，则； ④若
其中正确的命题是（）

将棱长为2的正方体木块削成一个体积最大的球，则这个球的表面积为（）

如图是某几何体的三视图，其中正视图是腰长为2的等腰三角形，俯视图是半径为1的半圆，则该几何体的体积是( )

如图，右边几何体的正视图和侧视图可能正确的是

图是一个几何体的三视图，根据图中数据，可得该几何体的表面积、体积分别是

A．32、	B．16、
C．12、	D．8、

已知一个四面体其中五条棱的长分别为1，1，1，1，，则此四面体体积的最大值是

过空间任意一点引三条不共面的直线，它们所确定的平面个数是( )

试题分类