题目内容
已知函数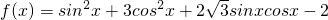 ,
,
(1)求函数f(x)的最大值及单调递减区间;
(2)若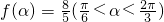 ,求cos2α的值.
,求cos2α的值.
解:(1)化简得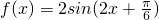 ,
,
当三角函数取到最大值时,函数式取到最大值2
故函数f(x)的最大值为2,
根据正弦函数的单调性可知当2x+
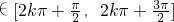 ,
,
∴x∈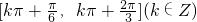 ;
;
∴单调递减区间为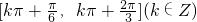 ;
;
(2)由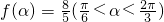
可得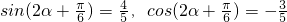 ,
,
∵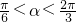 ,
,
∴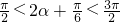 ,
,
∴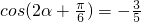
∴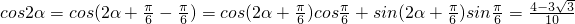 .
.
分析:(1)首先对所给的函数式进行整理,用二倍角公式再利用辅角公式,整理成能够进行性质运算的形式,函数的最大值可以通过函数的解析式直接做出,利用正弦函数的减区间整理出函数式的减区间
(2)根据所给的函数值,和所给的角的范围写出2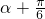 的范围,根据这个角的正弦值得到这个角的余弦值,通过角的变换,把要求的角写成已知角和特殊角的形式,利用两角差的余弦公式得到结果.
的范围,根据这个角的正弦值得到这个角的余弦值,通过角的变换,把要求的角写成已知角和特殊角的形式,利用两角差的余弦公式得到结果.
点评:本题考查三角函数的恒等变换,考查三角函数的有关性质的运算,注意本题中由函数值求函数值的过程中,角的范围的分析,这是解题的关键.
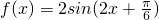 ,
,当三角函数取到最大值时,函数式取到最大值2
故函数f(x)的最大值为2,
根据正弦函数的单调性可知当2x+

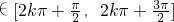 ,
,∴x∈
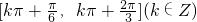 ;
;∴单调递减区间为
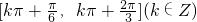 ;
;(2)由
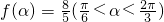
可得
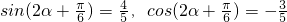 ,
,∵
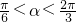 ,
,∴
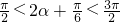 ,
,∴
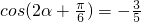
∴
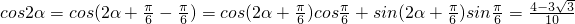 .
.分析:(1)首先对所给的函数式进行整理,用二倍角公式再利用辅角公式,整理成能够进行性质运算的形式,函数的最大值可以通过函数的解析式直接做出,利用正弦函数的减区间整理出函数式的减区间
(2)根据所给的函数值,和所给的角的范围写出2
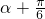 的范围,根据这个角的正弦值得到这个角的余弦值,通过角的变换,把要求的角写成已知角和特殊角的形式,利用两角差的余弦公式得到结果.
的范围,根据这个角的正弦值得到这个角的余弦值,通过角的变换,把要求的角写成已知角和特殊角的形式,利用两角差的余弦公式得到结果.点评:本题考查三角函数的恒等变换,考查三角函数的有关性质的运算,注意本题中由函数值求函数值的过程中,角的范围的分析,这是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.