题目内容
设直线![]() 双曲线
双曲线![]() ,双曲线的离心率为
,双曲线的离心率为![]() ,
,![]() 与
与![]() 交于
交于![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]()
(1)证明:![]() ;(2)求双曲线
;(2)求双曲线![]() 的方程;(3)若点
的方程;(3)若点![]() 是双曲线
是双曲线![]() 的右焦点,
的右焦点,![]() 是双曲线上两点,且
是双曲线上两点,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]() (Ⅲ)
(Ⅲ)![]()
解析:
(1)![]() 双曲线的离心率为
双曲线的离心率为![]() ,
,![]() ,从而
,从而![]() .双曲线的方程可化为
.双曲线的方程可化为![]() . 设
. 设![]()
由![]() 得:
得:![]()
则有![]() 从而
从而![]()
![]()
则![]() 即
即![]()
(2)![]() ,
, ![]()
 ,由
,由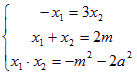 得
得![]()
由 得
得![]() 则
则![]()
故双曲线的方程为![]()
(3)易知![]() ,设
,设![]() .由
.由![]() 得:
得: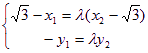
设直线![]() 的方程为
的方程为![]() .由
.由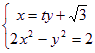 得:
得:![]()
则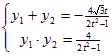 ,消去
,消去![]() 得:
得:![]()
![]() ,
, ![]() , 解得
, 解得![]() 或
或![]()
当![]() 时,可求出
时,可求出![]()
当直线![]() 与
与![]() 轴重合时,可求出
轴重合时,可求出![]() 或
或![]()
故![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
 与双曲线
与双曲线 交于A、B,且以AB为直径的圆过原点,求点
交于A、B,且以AB为直径的圆过原点,求点 的轨迹方程.
的轨迹方程.