题目内容
(本小题共13分)
在△ABC中,a,b,c分别为内角A,B,C的对边,且b2+c2-a2=bc.
(Ⅰ)求角A的大小;
(Ⅱ)设函数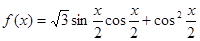 ,当
,当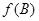 取最大值
取最大值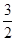 时,判断△ABC的形状.
时,判断△ABC的形状.
【答案】
解:(Ⅰ)在△ABC中,因为b2+c2-a2=bc,
由余弦定理 a2= b2+c2-2bccosA
可得cosA=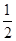 .(余弦定理或公式必须有一个,否则扣1分)
……3分
.(余弦定理或公式必须有一个,否则扣1分)
……3分
∵ 0<A<π , (或写成A是三角形内角) ……………………4分
∴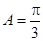 .
……………………5分
.
……………………5分
(Ⅱ)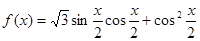
 ……………………7分
……………………7分
 ,
……………………9分
,
……………………9分
∵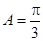 ∴
∴
∴ (没讨论,扣1分)
…………………10分
(没讨论,扣1分)
…………………10分
∴当 ,即
,即 时,
时, 有最大值是
有最大值是 .
……………………11分
.
……………………11分
又∵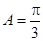 ,
∴
,
∴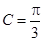
∴△ABC为等边三角形. ……………………13分
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. 在
在 处取得极值,求a的值;
处取得极值,求a的值; 在
在 上的最大值.
上的最大值. ,设函数
,设函数 .
. 在
在 上的单调递增区间;
上的单调递增区间; 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,
的对边, ,
, ,
, ,求边
,求边 ,求
,求
 的最小正周期及图象的对称轴方程式;
的最小正周期及图象的对称轴方程式; 的条件下,求
的条件下,求 的值.
的值.