题目内容
已知圆锥曲线mx2+4y2=4m的离心率e为方程2x2-5x+2=0的两根,则满足条件的圆锥曲线的条数为( )A.1
B.2
C.3
D.4
【答案】分析:方程2x2-5x+2=0的根是 和2当e=
和2当e= 时圆锥曲线mx2+4y2=4m是椭圆,当e=2时圆锥曲线mx2+4y2=4m是双曲线.由此能够推导出满足条件的圆锥曲线的条数.
时圆锥曲线mx2+4y2=4m是椭圆,当e=2时圆锥曲线mx2+4y2=4m是双曲线.由此能够推导出满足条件的圆锥曲线的条数.
解答:解:方程2x2-5x+2=0的根是 和2
和2
当e= 时圆锥曲线mx2+4y2=4m是椭圆,当e=2时圆锥曲线mx2+4y2=4m是双曲线.
时圆锥曲线mx2+4y2=4m是椭圆,当e=2时圆锥曲线mx2+4y2=4m是双曲线.
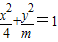 ,
,
若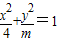 ,是椭圆,则c2=|4-m|,
,是椭圆,则c2=|4-m|,
e=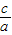 =
=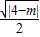 =
= 或
或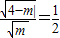 ,满足条件的圆锥曲线有2个;
,满足条件的圆锥曲线有2个;
若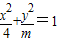 是双曲线,则m<0
是双曲线,则m<0
所以c2=4-m
e=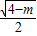 =2,满足条件的圆锥曲线有1个.
=2,满足条件的圆锥曲线有1个.
所以满足条件的圆锥曲线一共3条.
故选C.
点评:本题考查椭圆的双曲线的性质的简单应用,解题时要认真审题,仔细解答,注意熟练掌握基本概念,合理地进行等价转化.
 和2当e=
和2当e= 时圆锥曲线mx2+4y2=4m是椭圆,当e=2时圆锥曲线mx2+4y2=4m是双曲线.由此能够推导出满足条件的圆锥曲线的条数.
时圆锥曲线mx2+4y2=4m是椭圆,当e=2时圆锥曲线mx2+4y2=4m是双曲线.由此能够推导出满足条件的圆锥曲线的条数.解答:解:方程2x2-5x+2=0的根是
 和2
和2当e=
 时圆锥曲线mx2+4y2=4m是椭圆,当e=2时圆锥曲线mx2+4y2=4m是双曲线.
时圆锥曲线mx2+4y2=4m是椭圆,当e=2时圆锥曲线mx2+4y2=4m是双曲线.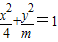 ,
,若
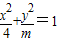 ,是椭圆,则c2=|4-m|,
,是椭圆,则c2=|4-m|,e=
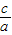 =
=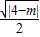 =
= 或
或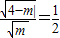 ,满足条件的圆锥曲线有2个;
,满足条件的圆锥曲线有2个;若
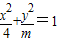 是双曲线,则m<0
是双曲线,则m<0所以c2=4-m
e=
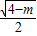 =2,满足条件的圆锥曲线有1个.
=2,满足条件的圆锥曲线有1个.所以满足条件的圆锥曲线一共3条.
故选C.
点评:本题考查椭圆的双曲线的性质的简单应用,解题时要认真审题,仔细解答,注意熟练掌握基本概念,合理地进行等价转化.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目