题目内容
在如图所示的几何体ABCED中，EC⊥面ABC，DB⊥面ABC，CE=CA=CB=2DB，∠ACB=90°，M为AD的中点．（1）证明：EM⊥AB；（2）求直线BM和平面ADE所成角的正弦值．
分析：（1）以C为原点建立如图所示的空间直角坐标系，根据
•
=0，得到
⊥
，从而有 EM⊥AB．
（2）由（1）知
的坐标，求出面ADE的法向量为
的坐标，设直线BM和平面ADE所成角为θ，则sinθ=|cos＜
，
＞=|
|．
| EM |
| AB |
| EM |
| AB |
（2）由（1）知
| BM |
| n |
| BM |
| n |
| ||||
|
|
解答：解：（1）证明：以C为原点建立如图所示的空间直角坐标系，设DB=1，则 CE=CA=CB=2．
由于A（2，0，0），B（0，2，0），E（0，0，2），D（0，2，1），M（1，1，
），∴
=（1，1-
），
=（-2，2，0），∴
•
=-2+2+0=0，∴
⊥
，∴EM⊥AB．
（2）由（1）知
=（1，-1，
），
=（-2，2，1），
=（-2，0，2），
=（0，-2，1）．
设面ADE的法向量为
=（x，y，z），则
，即
，
取
=（2，1，2）设直线BM和平面ADE所成角为θ，则 sinθ=|cos＜
，
＞=|
|=
．
由于A（2，0，0），B（0，2，0），E（0，0，2），D（0，2，1），M（1，1，
| 1 |
| 2 |
| EM |
| 3 |
| 2 |
| AB |
| EM |
| AB |
| EM |
| AB |
（2）由（1）知
| BM |
| 1 |
| 2 |
| AD |
| AE |
| DE |
设面ADE的法向量为
| n |
|
|
取
| n |
| BM |
| n |
| ||||
|
|
| 4 |
| 9 |
点评：本题考查两个向量垂直的条件，两个向量的夹角公式，体现了转化的数学思想，注意本题中sinθ=|cos＜
，
＞|．
| BM |
| n |
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
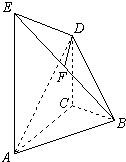在如图所示的几何体中，AE⊥平面ABC，CD∥AE，F是BE的中点，AC=BC=1，∠ACB=90°，AE=2CD=2．
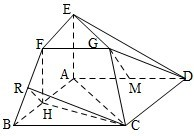在如图所示的几何体中，四边形ABCD为平行四边形，∠ACB=90°，EA⊥平面ABCD，EF∥AB，FG∥BC，EG∥AC．AB=2EF．
在如图所示的几何体中，平面ACE⊥平面ABCD，四边形ABCD为平行四边形，∠ACB=90°，EF∥BC，AC=BC=2EF，
（2012•宝鸡模拟）在如图所示的几何体中，四边形ACC1A1是矩形，FC1∥BC，EF∥A1C1，∠BCC1=90°，点A、B、E、A1在一个平面内，AB=BC=CC1=2，
（2013•淄博二模）在如图所示的几何体中，△ABC是边长为2的正三角形，AE＞1，AE⊥平面ABC，平面BCD⊥平面ABC，BD=CD，且BD⊥CD．