题目内容
 如图,ABB1A1是圆台的轴截面,O1、O分别是上下底面圆的圆心,A1O1=1,AO=2,母线与底面成60°角,点C在底面圆周上,且AC=2
如图,ABB1A1是圆台的轴截面,O1、O分别是上下底面圆的圆心,A1O1=1,AO=2,母线与底面成60°角,点C在底面圆周上,且AC=2| 2 |
(1)圆台的侧面积和体积;
(2)异面直线A1C与OO1所成的角的正切值.
分析:(1)要求侧面积,则需求母线长,要求体积,则需求高,所以A1D⊥AO易知A1D垂直圆台底面,所以∠A1AD为母线与底面所成的角,于是在Rt△A1AD中求得母线和高,再由侧面积公式和体积公式求解.
(2)由(1)易知A1D∥OO1,连接CD,可知∠CA1D就是异面直线A1C与OO1所成的角,再求得CD即可.
(2)由(1)易知A1D∥OO1,连接CD,可知∠CA1D就是异面直线A1C与OO1所成的角,再求得CD即可.
解答: 解:(1)由已知A1O1=1,AO=2,作A1D⊥AO于点D,则AD=AO-A1O1=1,
解:(1)由已知A1O1=1,AO=2,作A1D⊥AO于点D,则AD=AO-A1O1=1,
因为轴截面ABB1A1垂直于圆台底面,所以A1D垂直圆台底面,
所以∠A1AD=60°,(3分)
于是在Rt△A1AD中,得A1A=2,A1D=
,
即圆台的母线长为2,高为
.(5分)
所以圆台的侧面积为S=π(1+2)×2=6π,
圆台的体积为V=
π(12+22+1×2)×
=
.(8分)
(2)由(1)可知A1D∥OO1,连接CD,
则∠CA1D就是异面直线A1C与OO1所成的角,(10分)
因为AO=CO=2,AC=2
,
所以∠AOC=90°,
又AD=DO=1,所以在Rt△COD中可得CD=
,
所以tan∠CA1D=
=
=
.(13分)
 解:(1)由已知A1O1=1,AO=2,作A1D⊥AO于点D,则AD=AO-A1O1=1,
解:(1)由已知A1O1=1,AO=2,作A1D⊥AO于点D,则AD=AO-A1O1=1,因为轴截面ABB1A1垂直于圆台底面,所以A1D垂直圆台底面,
所以∠A1AD=60°,(3分)
于是在Rt△A1AD中,得A1A=2,A1D=
| 3 |
即圆台的母线长为2,高为
| 3 |
所以圆台的侧面积为S=π(1+2)×2=6π,
圆台的体积为V=
| 1 |
| 3 |
| 3 |
7
| ||
| 3 |
(2)由(1)可知A1D∥OO1,连接CD,
则∠CA1D就是异面直线A1C与OO1所成的角,(10分)
因为AO=CO=2,AC=2
| 2 |
所以∠AOC=90°,
又AD=DO=1,所以在Rt△COD中可得CD=
| 5 |
所以tan∠CA1D=
| CD |
| A1D |
| ||
|
| ||
| 3 |
点评:本题主要考查圆台的结构特征,侧面积和体积的求法以及异面直线所成的角,同时,考查了作辅助线的能力和转化能力,属中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 如图所示,有公共边的两正方形ABB1A1与BCC1B1的边AB、BC均在平面α内,且∠ABC=60°,M是BC的中点,点N在C1C上.
如图所示,有公共边的两正方形ABB1A1与BCC1B1的边AB、BC均在平面α内,且∠ABC=60°,M是BC的中点,点N在C1C上. 如图,ABB1A1是圆台的轴截面,O1、O分别是上下底面圆的圆心,A1O1=1,AO=2,母线与底面成60°角,点C在底面圆周上,且
如图,ABB1A1是圆台的轴截面,O1、O分别是上下底面圆的圆心,A1O1=1,AO=2,母线与底面成60°角,点C在底面圆周上,且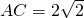 ,求:
,求: ,
,
 ,求:
,求: