Question

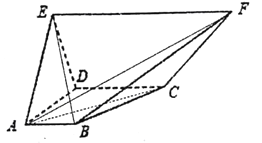
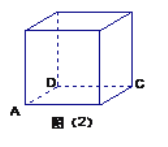
【题目】如图（1）是一正方体的表面展开图，MN和PB是两条面对角线，请在图（2）的正方体中将MN和PB画出来，并就这个正方体解决下面问题。

（1）求证：MN∥平面PBD；

（2）求证：平面；

（3）求PB和平面NMB所成的角的大小．

Answer 1

【答案】（1）见解析；（2）见解析；（3）

【解析】

由展开图还原出原图形，由正方体可证MN//DB,进一步证明MN∥平面PBD。通过证明平面,可证，同理可得，所以面PDB。连结BE,则为PB和平面NMB所成的角。

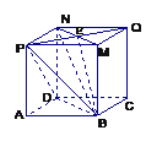
MN和PB的位置如右图示：

（1）∵ND∥MB 且ND＝MB，∴四边形NDBM为平行四边形

∴MN//DB

∵平面PDB,平面PDB

∴MN∥平面PBD

（2）∵平面ABCD，平面，∴

又∵ ∴平面,

面 ∴,同理可得,∵

∴面PDB

（3）连结PQ交MN于点E,

∵ ,

∴平面

连结BE,则为PB和平面NMB所成的角

在直角三角形PEB中∵ ∴=30°.

即PB和平面NMB所成的角为30°