题目内容

定义在（-∞，4]上的减函数f（x），使得f（m-sinx）≤f（ $数学公式$ - $数学公式$ +cos²x）对一切实数x均成立，则实数m的范围________．

$\text{[math]}$ ≤m≤3或m=- $\text{[math]}$
分析：根据已知条件定义在（-∞，4]上的减函数f（x），首先都要满足定义域小于等于4，然后根据减函数的性质列出不等式求出m的范围；
解答：∵减函数f（x）定义在（-∞，4]上，∴m-sinx≤4…①，
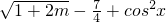$\text{[math]}$ ≤4…②，
∵1+2m≥0，∴m≥- $\text{[math]}$ ；
∵f（m-sinx）≤f（ $\text{[math]}$ - $\text{[math]}$ +cos²x）对一切实数x均成立，
∴m-sinx≥ 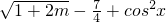$\text{[math]}$ …③，（m≥- $\text{[math]}$ ）
解①得，m≤4+sinx，∵-1≤sinx≤1，∴m≤3；
解②得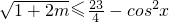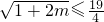， $\text{[math]}$ ，∴ $\text{[math]}$ ，解得m≤ $\text{[math]}$ ，
解③得，m- $\text{[math]}$ + $\text{[math]}$ ≥-sin²x-sinx=-（sinx+ $\text{[math]}$ ）²+ $\text{[math]}$ ，
∴（sinx+ $\text{[math]}$ ）²≥ $\text{[math]}$ -m- $\text{[math]}$ ，∵-1≤sinx≤1，
∴当sinx=- $\text{[math]}$ 时（sinx+ $\text{[math]}$ ）²取最小值为0，
∴0≥ $\text{[math]}$ -m- $\text{[math]}$ ，解得m≥ $\text{[math]}$ 或m=- $\text{[math]}$ ，
由①②③综合得： $\text{[math]}$ ≤m≤3或m=- $\text{[math]}$ ；
故答案为： $\text{[math]}$ ≤m≤3或m=- $\text{[math]}$
点评：此题主要考查函数的单调性与三角函数的性质，思路很简单但是计算很复杂，考查学生的计算能力，这一点在高考中均有体现，此题易错点忽视了定义域，1+2m≥0，这个条件不要忘记了；