题目内容
5.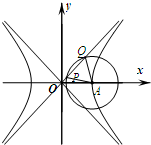 如图,已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q.若∠PAQ=60°且$\overrightarrow{OQ}$=4$\overrightarrow{OP}$,则双曲线C的离心率为( )
如图,已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q.若∠PAQ=60°且$\overrightarrow{OQ}$=4$\overrightarrow{OP}$,则双曲线C的离心率为( )| A. | $\sqrt{3}$ | B. | $\frac{2\sqrt{13}}{5}$ | C. | $\frac{\sqrt{7}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 确定△QAP为等边三角形,设AQ=2R,则,OP=$\frac{2}{3}$R,利用勾股定理,结合余弦定理和离心率公式,计算即可得出结论.
解答 解:因为∠PAQ=60°且$\overrightarrow{OQ}$=4$\overrightarrow{OP}$,
所以△QAP为等边三角形,
设AQ=2R,则PQ=2R,OP=$\frac{2}{3}$R,
渐近线方程为y=$\frac{b}{a}$x,A(a,0),
取PQ的中点M,则AM=$\frac{|ab|}{\sqrt{{a}^{2}+{b}^{2}}}$,
由勾股定理可得(2R)2-R2=($\frac{|ab|}{\sqrt{{a}^{2}+{b}^{2}}}$)2,
所以(ab)2=3R2(a2+b2)①,
在△OQA中,$\frac{(\frac{8}{3}R)^{2}+(2R)^{2}-{a}^{2}}{2•\frac{8}{3}R•2R}$=$\frac{1}{2}$,
所以$\frac{52}{9}$R2=a2②
①②结合c2=a2+b2,
可得e=$\frac{c}{a}$=$\frac{2\sqrt{13}}{5}$.
故选:B.
点评 本题考查双曲线的性质:离心率,考查余弦定理、勾股定理,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
15.若a,b,c均为实数,且ab<0,则下列不等式正确的是( )
| A. | |a+b|>|a-b| | B. | |a|+|b|>|a-b| | C. | |a-c|≤|a-b|+|b-c| | D. | |a-b|<|a|-|b| |
16.执行如图所示的程序框图,若a=1,b=2,则输出的结果是( )

| A. | 9 | B. | 11 | C. | 13 | D. | 15 |
10.四面体ABCD的四个顶点均在半径为2的球面上,若AB、AC、AD两两垂直,$\overrightarrow{BA}•\overrightarrow{BC}$=2,则该四面体体积的最大值为( )
| A. | $\frac{7\sqrt{2}}{6}$ | B. | $\frac{7}{3}$ | C. | 2$\sqrt{2}$ | D. | 7$\sqrt{2}$ |
15.执行如图所示的程序框图,会输出一列数,则这个数列的第3项是( )


| A. | 870 | B. | 30 | C. | 6 | D. | 3 |
 如图1,在边长为12的正方形AA′A${\;}_{1}^{′}$A1中,BB1∥CC1∥AA1,且AB=3,且BC=4,AA${\;}_{1}^{′}$分别交BB1,CC1于点P,Q,将该正方形沿BB1,CC1折叠,使得A′A${\;}_{1}^{′}$与AA1重合,构成图2所示的三棱柱ABC-A1B1C1,在图2中:
如图1,在边长为12的正方形AA′A${\;}_{1}^{′}$A1中,BB1∥CC1∥AA1,且AB=3,且BC=4,AA${\;}_{1}^{′}$分别交BB1,CC1于点P,Q,将该正方形沿BB1,CC1折叠,使得A′A${\;}_{1}^{′}$与AA1重合,构成图2所示的三棱柱ABC-A1B1C1,在图2中: