题目内容
在直角坐标系中, 为坐标原点,如果一个椭圆经过点P(3,
为坐标原点,如果一个椭圆经过点P(3, ),且以点F(2,0)为它的一个焦点.
),且以点F(2,0)为它的一个焦点.
(1)求此椭圆的标准方程;
(2)在(1)中求过点F(2,0)的弦AB的中点M的轨迹方程.
【答案】
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)既然是求椭圆的标准方程,那么另一个焦点必定是点 ,
, ,
, ,即
,即 ,
, ,可得椭圆标准方程为
,可得椭圆标准方程为 ;(2)只要知道本题中
;(2)只要知道本题中 (斜率存在时),利用这个等式可迅速求出结论,
(斜率存在时),利用这个等式可迅速求出结论,
试题解析:(1)设椭圆方程为: ,
,
则有: 解得:
解得: ,
,
故所求椭圆方程为 .
5分
.
5分
(2)设
则有 ,
,
两式相减,当 时,
时, ,又因为
,又因为 ,
,
∴ ,整理得:
,整理得: ,当
,当 时,中点
时,中点 满足上式.
满足上式.
综上所述,所求轨迹方程为 .10分
.10分
考点:(1)椭圆的标准方程;(2)轨迹方程.

练习册系列答案
相关题目
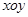 中,圆
中,圆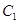 的参数方程为
的参数方程为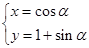 (
(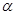 为参数)在极坐标系(与直角坐标系
为参数)在极坐标系(与直角坐标系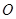 为极点,以
为极点,以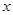 轴的正半轴为极轴)中,圆
轴的正半轴为极轴)中,圆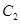 的极坐方程为
的极坐方程为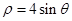 ,则
,则 (a >0)与x轴的正半轴交于点P.点Q的坐
(a >0)与x轴的正半轴交于点P.点Q的坐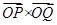 =6.
=6.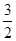 的直线交椭圆C于A、B两点,求△AOB的面积
的直线交椭圆C于A、B两点,求△AOB的面积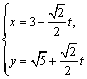 (
(