题目内容
设等差数列{an}的前n项和为Sn,已知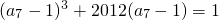 ,
,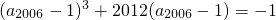 ,则下列结论正确的是
,则下列结论正确的是
- A.S2012=2012,a2012<a7
- B.S2012=2012,a2012>a7
- C.S2012=-2012,a2012<a7
- D.S2012=-2012,a2012>a7
A
分析:先确定等差数列的公差d<0,再将条件相加,结合等差数列的求和公式及等差数列的性质,即可求得结论.
解答:由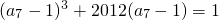 ,
,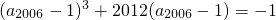 ,
,
可得a7-1>0,-1<a2006-1<0,即a7>1,0<a2006<1,从而可得等差数列的公差d<0
∴a2012<a7,
把已知的两式相加可得(a7-1)3+2012(a7-1)+(a2006-1)3+2012(a2006-1)=0
整理可得(a7+a2006-2)•[(a7-1)2+(a2006-1)2-(a7-1)(a2006-1)+2012]=0
结合上面的判断可知(a7-1)2+(a2006-1)2-(a7-1)(a2006-1)+2012>0
所以a7+a2006=2,而s2012= (a1+a2012)=
(a1+a2012)= (a7+a2006)=2012
(a7+a2006)=2012
故选A.
点评:本题考查了等差数列的性质的运用,灵活利用等差数列的性质是解决问题的关键,属于中档题.
分析:先确定等差数列的公差d<0,再将条件相加,结合等差数列的求和公式及等差数列的性质,即可求得结论.
解答:由
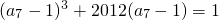 ,
,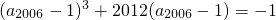 ,
,可得a7-1>0,-1<a2006-1<0,即a7>1,0<a2006<1,从而可得等差数列的公差d<0
∴a2012<a7,
把已知的两式相加可得(a7-1)3+2012(a7-1)+(a2006-1)3+2012(a2006-1)=0
整理可得(a7+a2006-2)•[(a7-1)2+(a2006-1)2-(a7-1)(a2006-1)+2012]=0
结合上面的判断可知(a7-1)2+(a2006-1)2-(a7-1)(a2006-1)+2012>0
所以a7+a2006=2,而s2012=
 (a1+a2012)=
(a1+a2012)= (a7+a2006)=2012
(a7+a2006)=2012故选A.
点评:本题考查了等差数列的性质的运用,灵活利用等差数列的性质是解决问题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目