题目内容
若 ,则
,则 的值是
的值是
- A.

- B.

- C.

- D.

B
分析:注意到sinθ与cosθ之间的关系,sin2θ+cos2θ=1,便得出方程组,解这个关于sinθ与cosθ的2元2次方程组,求得sinθ与cosθ,再得tanθ,最后利用和角公式求得 的值.
的值.
解答:∵sin2θ+cos2θ=1,
∴便得出方程组
解这个关于sinθ与cosθ的2元2次方程组,
∴ .所以tanθ=1.
.所以tanθ=1.
故有 .
.
答案:B.
点评:本题考查三角变换,解题的关键是联想公式的特点与结构,进行代换,从而转化为特殊角的三角函数,求出三角函数的值.
分析:注意到sinθ与cosθ之间的关系,sin2θ+cos2θ=1,便得出方程组,解这个关于sinθ与cosθ的2元2次方程组,求得sinθ与cosθ,再得tanθ,最后利用和角公式求得
 的值.
的值.解答:∵sin2θ+cos2θ=1,
∴便得出方程组

解这个关于sinθ与cosθ的2元2次方程组,
∴
 .所以tanθ=1.
.所以tanθ=1.故有
 .
.答案:B.
点评:本题考查三角变换,解题的关键是联想公式的特点与结构,进行代换,从而转化为特殊角的三角函数,求出三角函数的值.

练习册系列答案
相关题目
 ,
, .若
.若 ,则
,则 的值是( )
的值是( ) B.
B. C.
C. D.
D.
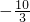

 ,若
,若