题目内容
【题目】在直角坐标系
中，直线
的参数方程为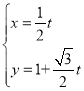
(t为参数)，以直角坐标系的
点为极点，
为极轴，且长度单位相同，建立极坐标系，得曲线
的极坐标方程为
.
（1）求直线的倾斜角；
（2）若直线与曲线交于
，
两点，求
的长度.
【答案】（1）
；（2）
【解析】
（1）利用消参法将直线
的参数方程化为普通方程，再利用斜率公式即可求出直线的倾斜角；
（2）利用互化公式
，
，
，将曲线
的极坐标方程化为直角坐标方程，再根据点到直线的距离公式，求出圆心
到直线的距离，最后再运用直线与圆的弦长公式
，即可求得结果.
解：（1）设直线的倾斜角为
，
∵直线的参数方程为
(t为参数)，所以
，
∴
，∵，
∴
，∴直线的倾斜角为，
（2）由曲线的极坐标方程为
，得
，
∵，，，
∴曲线的普通方程为
，
圆心为，半径
，
则圆心到直线的距离
，
∴
，
∴
的长度为.
练习册系列答案
相关题目
【题目】为了解某地网民浏览购物网站的情况，从该地随机抽取100名网民进行调查，其中男性、女性人数分别为45和55.下面是根据调查结果绘制的网民日均浏览购物网站时间的频率分布直方图，将日均浏览购物网站时间不低于40分钟的网民称为“网购达人”，已知“网购达人”中女性有10人.
（1）根据已知条件完成下面的
列联表，并判断是否有90%的把握认为是否为“网购达人”与性别有关；
非网购达人 | 网购达人 | 总计 | |
男 | |||
女 | 10 | ||
总计 |
（2）将上述调査所得到的频率视为概率，现在从该地的网民中随机抽取3名，记被抽取的3名网民中的“网购达人”的人数为X，求X的分布列、数学期望
和方差
.
参考公式：
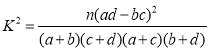，其中
.
参考数据：
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
