题目内容
已知函数f(x)= 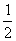
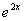 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数).
(1)讨论函数f(x)的单调性;
(2)若a=1,函数g(x)=(x-m)f(x)-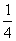
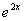 +x2+x在区间(0,+
+x2+x在区间(0,+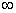 )上为增函数,求整数m 的最大值.
)上为增函数,求整数m 的最大值.
解:(Ⅰ)定义域为 ,
, ,
,
当 时,
时, ,所以
,所以 在
在 上为增函数;………………2分
上为增函数;………………2分
当 时,由
时,由 得
得 ,且当
,且当 时,
时, ,
,
当 时
时 ,
,
所以 在
在 为减函数,在
为减函数,在 为增函数.……………6分
为增函数.……………6分
(Ⅱ)当 时,
时, ,若
,若 在区间
在区间 上为增函数,
上为增函数,
则 在
在 恒成立,
恒成立,
即 在
在 恒成立 ………………8分
恒成立 ………………8分
令 ,
, ;
;  ,
, ;
;
令 ,可知
,可知 ,
, ,
,
又当 时
时 ,
,
所以函数 在
在 只有一个零点,设为
只有一个零点,设为 ,即
,即 ,
,
且 ;…………9分
;…………9分
由上可知当 时
时 ,即
,即 ;当
;当 时
时 ,即
,即 ,
,
所以 ,
, ,有最小值
,有最小值 ,…………10分
,…………10分
把 代入上式可得
代入上式可得 ,又因为
,又因为 ,所以
,所以 ,
,
又 恒成立,所以
恒成立,所以 ,又因为
,又因为 为整数,
为整数,
所以 ,所以整数
,所以整数 的最大值为1.…
的最大值为1.…

练习册系列答案
相关题目
 的数学期望和方差.
的数学期望和方差. 直角坐标方程为_
直角坐标方程为_ 
 ,过其焦点且斜率为-1的直线交抛物线于
,过其焦点且斜率为-1的直线交抛物线于 两点,若线段
两点,若线段 的中点的横坐标为3,则该抛物线的准线方程为( )
的中点的横坐标为3,则该抛物线的准线方程为( ) B.
B. C.
C. D.
D.
 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线 的方程为
的方程为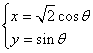 (
(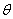 为参数),曲线
为参数),曲线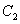 的极坐标方程为
的极坐标方程为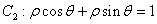 ,若曲线
,若曲线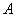 、
、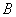 两点.
两点.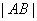 的值; (2)求点
的值; (2)求点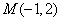 到
到 有大于零的极值点,则实数
有大于零的极值点,则实数 的取值范围是( )
的取值范围是( ) B
B  C
C  D
D 
 上的函数
上的函数 ,其导函数为
,其导函数为 ,且
,且 恒成立,
恒成立, B
B C
C D
D
 的顶点为
的顶点为 ,与
,与 轴正半轴的交点为
轴正半轴的交点为 ,设抛物线与两坐标轴正半轴围成的区域为
,设抛物线与两坐标轴正半轴围成的区域为 ,随机往
,随机往 , 则点
, 则点 内的概率是( )
内的概率是( )








 ,则
,则 ( )
( )