题目内容
已知向量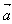 =(cos(x+
=(cos(x+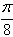 ),sin2(x+
),sin2(x+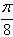 )),
)),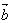 =(sin(x+
=(sin(x+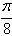 ),1),函数f(x)=
),1),函数f(x)=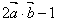 。
。
(1)求函数f(x)的解析式,并写出函数图象的对称中心坐标与对称轴方程;
(2)求函数y=f(- x)的单调递增区间。
x)的单调递增区间。
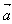 =(cos(x+
=(cos(x+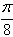 ),sin2(x+
),sin2(x+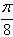 )),
)),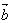 =(sin(x+
=(sin(x+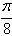 ),1),函数f(x)=
),1),函数f(x)=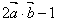 。
。(1)求函数f(x)的解析式,并写出函数图象的对称中心坐标与对称轴方程;
(2)求函数y=f(-
 x)的单调递增区间。
x)的单调递增区间。解:(1)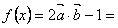
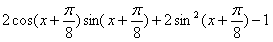
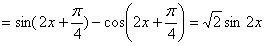
令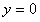 ,即
,即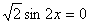
得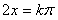 ,
,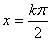 ,
,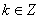
对称点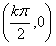 ,k∈Z
,k∈Z
由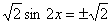
∴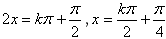 ,k∈Z
,k∈Z
对称轴方程是直线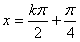 ,
,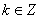 ;
;
(2)∵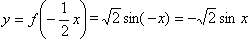
∴函数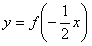 的单调递增区间是
的单调递增区间是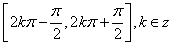
单调递减区间是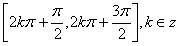 。
。
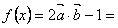
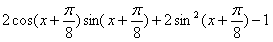
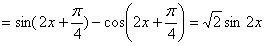
令
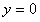 ,即
,即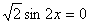
得
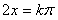 ,
,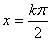 ,
,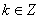
对称点
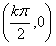 ,k∈Z
,k∈Z由
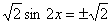
∴
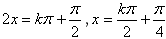 ,k∈Z
,k∈Z对称轴方程是直线
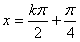 ,
,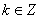 ;
;(2)∵
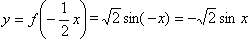
∴函数
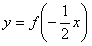 的单调递增区间是
的单调递增区间是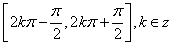
单调递减区间是
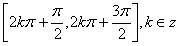 。
。
练习册系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |