题目内容
等差数列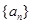 的前
的前 项和为
项和为 ,且
,且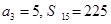 .
.
(1)数列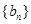 满足:
满足: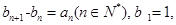 求数列
求数列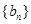 的通项公式;
的通项公式;
(2)设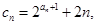 求数列
求数列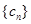 的前
的前 项和
项和
(1) ;(2)
;(2)
解析试题分析:(1)设等差数列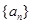 的公差为
的公差为 ,由已知得
,由已知得 ,解得
,解得 ,
,
从而求出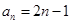 ,又
,又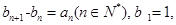 所以
所以
 ;
;
(2)由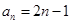 可知
可知 ,利用分组求和法求出
,利用分组求和法求出 .
.
试题解析:(1)设等差数列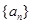 的公差为
的公差为 ,由已知
,由已知
解得:
∴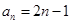
又

(2)
∴

考点:等差数列的通项公式与求和公式以及数列求和

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
题目内容
等差数列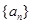 的前
的前 项和为
项和为 ,且
,且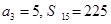 .
.
(1)数列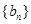 满足:
满足: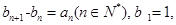 求数列
求数列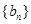 的通项公式;
的通项公式;
(2)设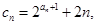 求数列
求数列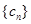 的前
的前 项和
项和
(1) ;(2)
;(2)
解析试题分析:(1)设等差数列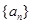 的公差为
的公差为 ,由已知得
,由已知得 ,解得
,解得 ,
,
从而求出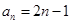 ,又
,又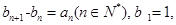 所以
所以
 ;
;
(2)由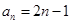 可知
可知 ,利用分组求和法求出
,利用分组求和法求出 .
.
试题解析:(1)设等差数列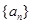 的公差为
的公差为 ,由已知
,由已知
解得:
∴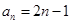
又

(2)
∴

考点:等差数列的通项公式与求和公式以及数列求和

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案