题目内容
已知函数 ,
,
(1)讨论f(x)的奇偶性,并证明你的结论;
(2)当f(x)是奇函数时,求f(x)在[-c,c](c>0,c是常数)上的值域.
解:(1)当a=0时, ,∴
,∴ ,故f(x)为奇函数.(2分).
,故f(x)为奇函数.(2分).
当a≠0时,f(a)=0, ,∴f(-a)≠f(a),且f(-a)≠-f(a),
,∴f(-a)≠f(a),且f(-a)≠-f(a),
故f(x)为非奇非偶函数.(4分).
(2)当a=0时, 为奇函数,
为奇函数, ,令f'(x)=0,得x=±2.
,令f'(x)=0,得x=±2.
当x变化时f'(x)与f(x)的变化情况如下表:
又当x<0时,f(x)<0;当x>0时,f(x)<0.
故f(x)(x∈R)的最大值为 ;f(x)(x∈R)的最小值为
;f(x)(x∈R)的最小值为 .(8分).
.(8分).
由上可知当x∈[-c,c](c>0)时,
(1)若0<c≤2,则f(x)在[-c,c](c>0)上单调递增,所以f(x)的值域为 (10分).
(10分).
(2)若c>2,则f(x)在[-c,-2]上单调递减,在[-2,2]上单调递增,在[2,c]上单调递减,所以f(x)的值域为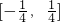 .(12分)
.(12分)
分析:(1)分类讨论,利用函数奇偶性的定义,可得结论;
(2)求导函数,确定函数的单调性,分类讨论,可得函数的值域.
点评:本题考查函数的奇偶性,考查导数知识的运用,考查函数的值域,考查学生的计算能力,属于中档题.
 ,∴
,∴ ,故f(x)为奇函数.(2分).
,故f(x)为奇函数.(2分).当a≠0时,f(a)=0,
 ,∴f(-a)≠f(a),且f(-a)≠-f(a),
,∴f(-a)≠f(a),且f(-a)≠-f(a),故f(x)为非奇非偶函数.(4分).
(2)当a=0时,
 为奇函数,
为奇函数, ,令f'(x)=0,得x=±2.
,令f'(x)=0,得x=±2.当x变化时f'(x)与f(x)的变化情况如下表:
| x | (-∞,-2) | -2 | (-2,2) | 2 | (2,+∞) |
| f'(x) | - | 0 | + | 0 | - |
| f(x) | 递减 | 极小值 | 递增 | 极大值 | 递减 |
故f(x)(x∈R)的最大值为
 ;f(x)(x∈R)的最小值为
;f(x)(x∈R)的最小值为 .(8分).
.(8分).由上可知当x∈[-c,c](c>0)时,
(1)若0<c≤2,则f(x)在[-c,c](c>0)上单调递增,所以f(x)的值域为
 (10分).
(10分).(2)若c>2,则f(x)在[-c,-2]上单调递减,在[-2,2]上单调递增,在[2,c]上单调递减,所以f(x)的值域为
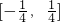 .(12分)
.(12分)分析:(1)分类讨论,利用函数奇偶性的定义,可得结论;
(2)求导函数,确定函数的单调性,分类讨论,可得函数的值域.
点评:本题考查函数的奇偶性,考查导数知识的运用,考查函数的值域,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
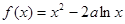 ,
,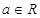
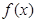 单调区间;
单调区间;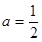 时,证明:当
时,证明:当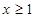 时,证明:
时,证明: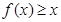 。
。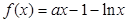
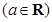 .
.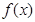 在定义域内的极值点的个数;
在定义域内的极值点的个数; 处取得极值,对
处取得极值,对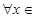
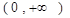 ,
,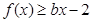 恒成立,求实数
恒成立,求实数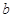 的取值范围.
的取值范围. 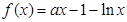
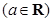 .
.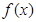 在定义域内的极值点的个数;
在定义域内的极值点的个数;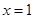 处取得极值,对
处取得极值,对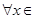
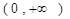 ,
,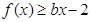 恒成立,求实数
恒成立,求实数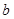 的取值范围;
的取值范围;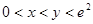 且
且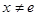 时,试比较
时,试比较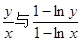 的大小.
的大小. .
. 函数
函数 的单调性;
的单调性; 为偶数时,正项数列
为偶数时,正项数列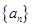 满足
满足 ,求
,求 时,求证:
时,求证: .
. 。(1)讨论函数
。(1)讨论函数 的单调性;(2)当
的单调性;(2)当 时,设
时,设 ,若
,若 时,
时, 恒成立。求整数
恒成立。求整数 的最大值。
的最大值。