题目内容
已知函数f(x)=6lnx-ax2-8x+b,其中a,b为常数且x=3是f(x)的一个极值点.(1)求a的值;
(2)求函数f(x)的单调减区间;
(3)若y=f(x)的图象与x轴有且只有3个交点,求b的取值范围.
【答案】分析:(1)由函数的解析式,可求出函数导函数的解析式,进而根据x=3是f(x)的一个极值点f′(3)=0,可构造关于a的方程,求出a值;
(2)由(1)可得函数导函数的解析式,分析导函数值大于0和小于0时,x的范围,可得函数f(x)的单调减区间;
(3)若y=f(x)的图象与x轴有且只有3个交点,则函数的极大值与极小值异号,进而构造关于b的不等式,解不等式可得答案.
解答:解:(1)∵f(x)=6lnx-ax2-8x+b,
∴f′(x)=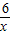 -2ax-8,
-2ax-8,
又∵x=3是f(x)的一个极值点
∴f′(3)=2-6a-8=0,
则a=-1.
(2)函数f(x)的定义域为(0,+∞).
由(I)知f(x)=6lnx+x2-8+b.
∴f′(x)=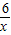 +2x-8=
+2x-8=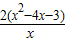 .
.
由f′(x)>0可得x>3或x<1,由f′(x)<0可得1<x<3.
∴函数f(x)的单调递增区间为(0,1)和(3,+∞),单调递减区间为(1,3).
(3)由(Ⅱ)可知函数f(x)在(0,1)单调递增,在(1,3)单调递减,在(3,+∞)单调递增.
且当x=1或x=3时,f′(x)=0.
∴f′(x)的极大值为f(1)=6ln1+1-8+b=b-7,
f′(x)的极大值为f(3)=6ln3+9-24+b=6ln3+b-15.
∵当x充分接近0时,f′(x)<0.当x充分大时,f(x)>0.
∴要使的f′(x)图象与x轴正半轴有且仅有三个不同的交点,只
需f(1)•f(3)<0
即(b-7)•(6ln3+b-15)<0
解得:7<b<15-6ln3
点评:本题考查的知识点是利用导数研究函数的极值,利用导数研究函数的单调性,其中根据已知条件确定a值,得到函数导函数的解析式并对其符号进行分析,是解答的关键.
(2)由(1)可得函数导函数的解析式,分析导函数值大于0和小于0时,x的范围,可得函数f(x)的单调减区间;
(3)若y=f(x)的图象与x轴有且只有3个交点,则函数的极大值与极小值异号,进而构造关于b的不等式,解不等式可得答案.
解答:解:(1)∵f(x)=6lnx-ax2-8x+b,
∴f′(x)=
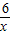 -2ax-8,
-2ax-8,又∵x=3是f(x)的一个极值点
∴f′(3)=2-6a-8=0,
则a=-1.
(2)函数f(x)的定义域为(0,+∞).
由(I)知f(x)=6lnx+x2-8+b.
∴f′(x)=
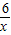 +2x-8=
+2x-8=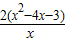 .
.由f′(x)>0可得x>3或x<1,由f′(x)<0可得1<x<3.
∴函数f(x)的单调递增区间为(0,1)和(3,+∞),单调递减区间为(1,3).
(3)由(Ⅱ)可知函数f(x)在(0,1)单调递增,在(1,3)单调递减,在(3,+∞)单调递增.
且当x=1或x=3时,f′(x)=0.
∴f′(x)的极大值为f(1)=6ln1+1-8+b=b-7,
f′(x)的极大值为f(3)=6ln3+9-24+b=6ln3+b-15.
∵当x充分接近0时,f′(x)<0.当x充分大时,f(x)>0.
∴要使的f′(x)图象与x轴正半轴有且仅有三个不同的交点,只
需f(1)•f(3)<0
即(b-7)•(6ln3+b-15)<0
解得:7<b<15-6ln3
点评:本题考查的知识点是利用导数研究函数的极值,利用导数研究函数的单调性,其中根据已知条件确定a值,得到函数导函数的解析式并对其符号进行分析,是解答的关键.

练习册系列答案
相关题目
 已知函数f(x)=Acos(ωx+φ)(x∈R)的图象的一部分如图所示,其A>0,ω>0,|φ|<
已知函数f(x)=Acos(ωx+φ)(x∈R)的图象的一部分如图所示,其A>0,ω>0,|φ|<