题目内容
已知不重合的两个点P(1,cosx),Q(cosx,1) ,O为坐标原点.
,O为坐标原点.(1)求
 夹角的余弦值f(x)的解析式及其值域;
夹角的余弦值f(x)的解析式及其值域;(2)求△OPQ的面积S(x),并求出其取最大值时,
 的值.
的值.
【答案】分析:(1)由已知中点P(1,cosx),Q(cosx,1)的坐标,进而根据cosθ=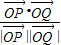 ,我们可以求出余弦值f(x)的解析式,结合
,我们可以求出余弦值f(x)的解析式,结合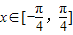 及对勾函数的单调性,易得到函数f(x)的值域;
及对勾函数的单调性,易得到函数f(x)的值域;
(2)由(1)中结论,代入△OPQ的面积公式,我们易确定出函数S(x)的表达式,进而根据及求出面积S(x)的最大值,及对应的x值,代入即可求出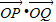 的值.
的值.
解答:解:(1)cosθ=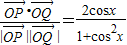 ,
,
∵P,Q不重合,∴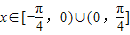 ,…(2分)
,…(2分)
∵cosx>0,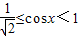 ,因此f(x)=
,因此f(x)=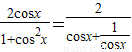 ,…(4分)
,…(4分)
由函数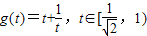 的单调性,得
的单调性,得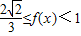 .…(6分)
.…(6分)
(2)S(x)=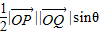 =
=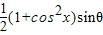
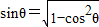 =
=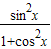 …(8分)
…(8分)
∴S(x)=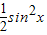 ,
,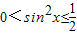 ,…(10分)
,…(10分)
当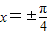 ,S(x)取最大值
,S(x)取最大值 ,
,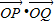 =2
=2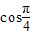 =
=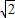 .…(12分)
.…(12分)
点评:本题考查的知识点是平面向量的数量积的坐标表示,平面向量数量积的运算,其中(1)的关键是确定出f(x)的解析式,(2)的关键是函数S(x)的表达式.
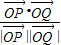 ,我们可以求出余弦值f(x)的解析式,结合
,我们可以求出余弦值f(x)的解析式,结合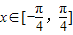 及对勾函数的单调性,易得到函数f(x)的值域;
及对勾函数的单调性,易得到函数f(x)的值域;(2)由(1)中结论,代入△OPQ的面积公式,我们易确定出函数S(x)的表达式,进而根据及求出面积S(x)的最大值,及对应的x值,代入即可求出
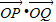 的值.
的值.解答:解:(1)cosθ=
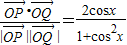 ,
,∵P,Q不重合,∴
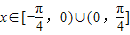 ,…(2分)
,…(2分)∵cosx>0,
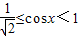 ,因此f(x)=
,因此f(x)=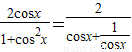 ,…(4分)
,…(4分)由函数
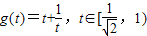 的单调性,得
的单调性,得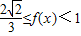 .…(6分)
.…(6分)(2)S(x)=
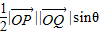 =
=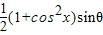
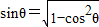 =
=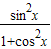 …(8分)
…(8分)∴S(x)=
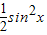 ,
,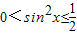 ,…(10分)
,…(10分)当
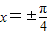 ,S(x)取最大值
,S(x)取最大值 ,
,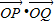 =2
=2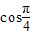 =
=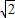 .…(12分)
.…(12分)点评:本题考查的知识点是平面向量的数量积的坐标表示,平面向量数量积的运算,其中(1)的关键是确定出f(x)的解析式,(2)的关键是函数S(x)的表达式.

练习册系列答案
相关题目
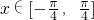 ,O为坐标原点.
,O为坐标原点. 夹角的余弦值f(x)的解析式及其值域;
夹角的余弦值f(x)的解析式及其值域; 的值.
的值. ,O为坐标原点.
,O为坐标原点. 夹角的余弦值f(x)的解析式及其值域;
夹角的余弦值f(x)的解析式及其值域; 的值.
的值.