题目内容
已知 是定义在R上不恒为零的偶函数,且对任意
是定义在R上不恒为零的偶函数,且对任意 ,都有
,都有 ,则
,则 的值是( )
的值是( )
| A.0 | B.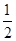 | C.1 | D. |
A
解析试题分析:因为函数f(x)是定义在R上不恒为零的偶函数,那么可知f(x)=f(-x),同时又xf(x+1)=(x+1)f(x),那么可知函数令x=-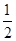 ,则可知-
,则可知-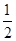 f(
f(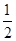 )=
)=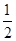 f(-
f(-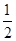 ),解得f(
),解得f(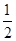 )=0,将x=
)=0,将x=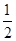 ,代入得到f(
,代入得到f( 0,同理依次得到f(
0,同理依次得到f( )=0,故选A.
)=0,故选A.
考点:本题主要考查了函数的奇偶性的运用,以及函数值的求解。
点评:解决该试题的关键是利用函数的主条件用递推的方法求函数值,将条件和结论有机地结合起来,作适当变形,把握递推的规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
f (x)= (n∈Z)是偶函数,且y=f(x)在(0,+∞)上是减函数,则n=( ).
(n∈Z)是偶函数,且y=f(x)在(0,+∞)上是减函数,则n=( ).
| A.1 | B.2 | C.1或2 | D.3 |
下图是函数f(x)的图象,它与x轴有4个不同的公共点.给出下列四个区间之中,存在不能用二分法求出的零点,该零点所在的区间是( )
| A.[-2.1,-1] | B.[4.1,5] |
| C.[1.9,2.3] | D.[5,6.1] |
规定 表示
表示 两个数中的最小的数,若函数
两个数中的最小的数,若函数 的图像关于直线
的图像关于直线 对称,则
对称,则 的值是( )
的值是( )
A. | B. | C. | D. |
下列各组函数中,表示同一函数的是
A. , , |
B. , ,  |
C. , ,  = = |
D. = = × × , , = = |
已知 ,
, ,
,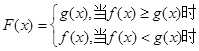 ,则
,则 的最值是( )
的最值是( )
A.最大值为3,最小值 | B.最大值为 ,无最小值 ,无最小值 |
| C.最大值为3,无最小值 | D.既无最大值,也无最小值 |
 的定义域为开区间
的定义域为开区间 ,导函数
,导函数 在
在
 、
、 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当 时,
时, ,且
,且 ,则不等式
,则不等式 0的解集是( )
0的解集是( )



