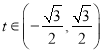题目内容
【题目】已知命题![]() ,
,![]() ;命题
;命题![]() 关于
关于![]() 的方程
的方程![]() 有两个相异实数根.
有两个相异实数根.
(1)若![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 为真命题,
为真命题,![]() 为假命题,求实数
为假命题,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题首先结合对数函数二次函数性质求解命题p,q为真命题时的m的取值范围,(1)中由![]() 为真命题可知p假q真,由此解不等式可求得实数
为真命题可知p假q真,由此解不等式可求得实数![]() 的取值范围;(2)中
的取值范围;(2)中![]() 为真命题,
为真命题,![]() 为假命题可知两命题一真一假,分两种情况可分别求得m的取值范围
为假命题可知两命题一真一假,分两种情况可分别求得m的取值范围
试题解析:令![]() ,则
,则![]() 在[0,2]上是增函数,
在[0,2]上是增函数,
故当![]() 时,
时,![]() 最小值为
最小值为![]() ,故若
,故若![]() 为真,则
为真,则![]() . ……2分
. ……2分
![]() 即
即![]() 时,方程
时,方程![]() 有两相异实数根,
有两相异实数根,
∴![]() ; ……4分
; ……4分
(1)若![]() 为真,则实数
为真,则实数![]() 满足
满足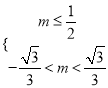 故
故![]() ,
,
即实数![]() 的取值范围为
的取值范围为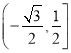 ……8分
……8分
(2)若![]() 为真命题,
为真命题,![]() 为假命题,则
为假命题,则![]() 一真一假,
一真一假,
若![]() 真
真![]() 假,则实数
假,则实数![]() 满足
满足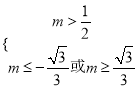 即
即![]() ;
;
若![]() 假
假![]() 真,则实数
真,则实数![]() 满足
满足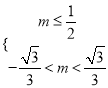 即
即![]() .
.
综上所述,实数![]() 的取值范围为
的取值范围为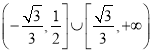 . ……12[来源:学&
. ……12[来源:学&

练习册系列答案
相关题目