题目内容
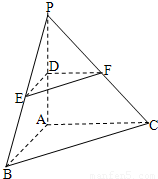
平面ABC⊥平面BCD,∠BDC=90°,AB⊥CD,E、F分别是AD、BC的中点,若EF=CD,则EF与平面ABD所成的角是_____________.
答案:30°
解析:如图，
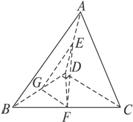
连结DF，取BD中点G，连结FG、EG，
△BDC为直角三角形且DF为斜边上的中线，
∴DF=
BC=BF.
∵G为BD中点,
∴GF⊥BD.又CD∥GF(中位线)且CD⊥AB，
∴GF⊥AB.∴GF⊥平面ABD.
∴∠GEF为EF与平面ABD所成的角.
在△EFG中，GF=
CD，EF=CD，
∴∠GEF=30°.
练习册系列答案
相关题目
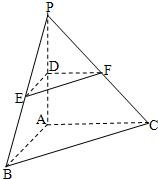如图，在三棱锥P-ABC中，PA⊥平面ABC，AB⊥AC，D、E、F分别是棱PA、PB、PC的中点，连接DE，DF，EF．
＝1，BC＝1，B
＝1，C
，平面ABC⊥平面BC
，E、F分别为棱AB、C
⊥平面
．
＝1，BC＝1，B
＝1，C
＝
，平面ABC⊥平面BC
，E、F分别为棱AB、C
；
⊥平面
．
