题目内容
甲、乙两人破译一密码,他们能破译的概率分别为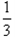 和
和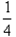 ,求:
,求:
(1)两人都能破译的概率;
(2)两人都不能破译的概率;
(3)恰有一人能破译的概率;
(4)至多有一人能破译的概率;
(5)若要使破译的概率为99%,至少需要多少个乙这样的人?
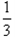 和
和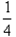 ,求:
,求:(1)两人都能破译的概率;
(2)两人都不能破译的概率;
(3)恰有一人能破译的概率;
(4)至多有一人能破译的概率;
(5)若要使破译的概率为99%,至少需要多少个乙这样的人?
解:设“甲能破译”为事件A,“乙能破译”为事件B,
则A、B相互独立,
从而A与 与B
与B 与
与 均相互独立,
均相互独立,
(1)“两人都能破译”为事件AB,
则P(A·B)=P(A)· ;
;
(2)“两人都不能破译”为事件 ,
,
则
 ;
;
(3)“恰有一人能破译”为事件 ,
,
又 与
与 互斥,
互斥,
则

 ;
;
(4)“至多一人能破译”为事件 ,
,
且 互斥,
互斥,
故



 ;
;
(5)设至少需n个乙这样的人,而n个乙这样的人都不能破译的概率为 ,
,
故n个乙这样的人能破译的概率为 =99%,
=99%,
解得n=16,
故至少需16个乙这样的人,才能使破译的概率为99%。
则A、B相互独立,
从而A与
 与B
与B 与
与 均相互独立,
均相互独立,(1)“两人都能破译”为事件AB,
则P(A·B)=P(A)·
 ;
;(2)“两人都不能破译”为事件
 ,
,则

 ;
;(3)“恰有一人能破译”为事件
 ,
,又
 与
与 互斥,
互斥,则


 ;
;(4)“至多一人能破译”为事件
 ,
,且
 互斥,
互斥,故




 ;
;(5)设至少需n个乙这样的人,而n个乙这样的人都不能破译的概率为
 ,
,故n个乙这样的人能破译的概率为
 =99%,
=99%,解得n=16,
故至少需16个乙这样的人,才能使破译的概率为99%。

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目