题目内容
(本小题满分12)如图①在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E,F,G分别是线段PC、PD,BC的中点,现将ΔPDC折起,使PD⊥平面ABCD(如图②)
(1)求证AP∥平面EFG;
(2)求平面EFG与平面PDC所成角的大小;
(3)求点A到平面EFG的距离。

【答案】
解法一:(Ⅰ)如图. 以D为坐标原点,直线DA、DC、DP分别为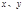 与z轴建立空间直角坐标系:
与z轴建立空间直角坐标系:
则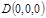
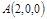
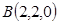
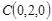
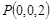
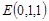
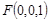
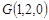
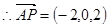
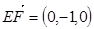
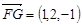
设平面GEF的法向量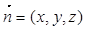 ,由法向量的定义得:
,由法向量的定义得:
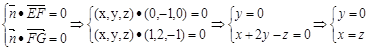
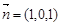 不妨设 z=1,
则
不妨设 z=1,
则
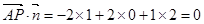
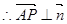 ,点P
,点P 平面EFG
平面EFG
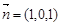 ∴AP∥平面EFG
∴AP∥平面EFG
(Ⅱ)由(Ⅰ)知平面GEF的法向量 ,
因平面EFD与坐标平面PDC重合 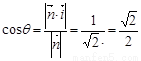 ,则它的一个法向量为
,则它的一个法向量为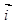 =(1,0,0)
=(1,0,0)
设平面间的夹角为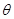 . 则
. 则
故夹角的大小为45°。
(Ⅲ)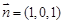 ,
,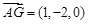
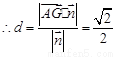
解法二:(1)∵EF∥CD∥AB,EG∥PB,根据面面平行的判定定理
∴平面EFG∥平面PAB,又PA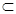 面PAB,∴AP∥平面EFG
面PAB,∴AP∥平面EFG
(2)∵平面PDC⊥平面ABCD,AD⊥DC
∴AD⊥平面PCD,而BC∥AD,∴BC⊥面EFD
过C作CR⊥EF交EF延长线于R点连GR,根据三垂线定理知
∠GRC即为二面角的平面角,∵GC=CR,∴∠GRC=45°,
故平面间的夹角大小为45°。 (3)同上
【解析】略

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
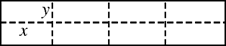
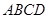 和矩形
和矩形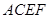 所在的平面相互垂直,已知
所在的平面相互垂直,已知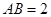 ,
,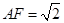 .
.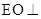 平面
平面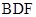 ;
;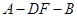 的大小.
的大小.
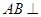 底面
底面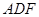 ,底面
,底面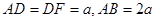 ,M、G分别是AB、DF的中点.
,M、G分别是AB、DF的中点. 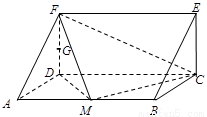
 中,E、F分别是中点。
中,E、F分别是中点。 ;
; ;
;
 上是否存在点P使
上是否存在点P使 ,若存在,确定点P位置;若不存在,说明理由。
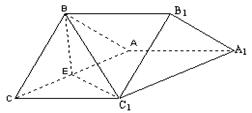
,若存在,确定点P位置;若不存在,说明理由。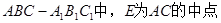 .
.
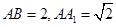 ,求点
,求点 到平面
到平面 的距离;
的距离;
 为何值时,二面角
为何值时,二面角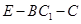 的正弦值为
的正弦值为 ?
?