题目内容
在边长为3的正三角形ABC中,E、F、G分别是AB、BC、CA边上的点,满足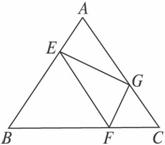
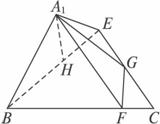
图1 图2
(1)求证:EG⊥A1B;
(2)求直线A1B与平面BEF所成的角;
(3)求四棱锥A1—BCGE的体积.
答案:(1)证明:在图1中AE=1,CF=CG=1,EB=BF=AG=2.
在△AEG中,AE=1,AG=2,∠A=60°.
∴EG2=12+22-2×1×2cos60°=3=AG2-AE2,
∴△AEG是直角三角形,AE⊥EG,BE⊥EG,于是图2中A1E⊥EG,BE⊥EG,又A1E∩BE=E.
∴EG⊥平面A1BE,又∵A1B![]() 平面A1BE,
平面A1BE,
∴EG⊥A1B.


图1 图2
(2)解:∵A1E⊥EG,BE⊥EG,∴∠A1EB是二面角A1EGB的平面角.由题设,∠A1EB=60°.
在△A1BE中,A1E=1,BE=2,∠A1EB=60°,∴A1B2=12+22-2×1×2cos60°=3=BE2-A1E2,
∴△A1BE是直角三角形,∴∠EA1B=90°.5分
作A1H⊥BE于H.
∵EG⊥平面A1BE,又A1H![]() 平面A1BE,
平面A1BE,
∴EG⊥A1H.
又A1H⊥BE,EG∩BE=E,∴A1H⊥平面BEGF于H.
∴∠A1BH是直线A1B与平面BEF所成的角.
在Rt△A1BE中∠A1EB=60°,∴∠A1BH=30°.9分
(3)解:![]() A1H·SBCGE=
A1H·SBCGE=![]() A1H(S△ABC-S△AEG)=
A1H(S△ABC-S△AEG)=![]() .
.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
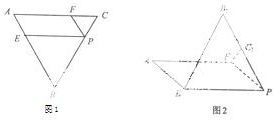 如图1,在边长为3的正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE=CF=CP=1,今将△BEP、△CFP分别沿EP、FP向上折起,使边BP与边CP所在的直线重合(如图2),B、C折后的对应点分别记为B、C1.
如图1,在边长为3的正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE=CF=CP=1,今将△BEP、△CFP分别沿EP、FP向上折起,使边BP与边CP所在的直线重合(如图2),B、C折后的对应点分别记为B、C1.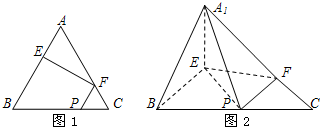 如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,
如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC, (2012•东城区一模)如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△AEF沿EF折起到△A1EF的位置,使平面A1EF⊥平面EFB,连接A1B,A1P.(如图2)
(2012•东城区一模)如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△AEF沿EF折起到△A1EF的位置,使平面A1EF⊥平面EFB,连接A1B,A1P.(如图2)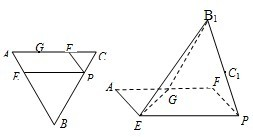 (2013•临沂三模)如图,在边长为3的正三角形ABC中,G、F为边AC的三等分点,E、P分别是AB、BC边上的点,满足AE=CP=1,今将△BEP,△CFP分别沿EP,FP向上折起,使边BP与边CP所在的直线重合,B,C折后的对应点分别记为B1,C1.
(2013•临沂三模)如图,在边长为3的正三角形ABC中,G、F为边AC的三等分点,E、P分别是AB、BC边上的点,满足AE=CP=1,今将△BEP,△CFP分别沿EP,FP向上折起,使边BP与边CP所在的直线重合,B,C折后的对应点分别记为B1,C1.