题目内容
若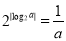
，则
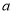的取值范围为________________.
【解析】
试题分析：当
时，
，则
，解得
；
当
时，
，则
恒成立，故；
综上可知.
考点：本题考查指数、对数的性质，分类讨论思想.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
天天向上一本好卷系列答案小学生10分钟应用题系列答案题目内容
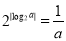若，则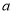的取值范围为________________.
【解析】
试题分析：当时，，则，解得；
当时，，则恒成立，故；
综上可知.
考点：本题考查指数、对数的性质，分类讨论思想.
天天向上一本好卷系列答案小学生10分钟应用题系列答案
