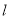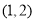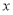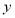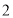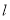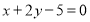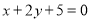题目内容
已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, .
.
(1)求 ;
;
(2)求 的解析式;
的解析式;
(3)若 ,求区间
,求区间 .
.
(1) ;(2)
;(2) ;(3)区间
;(3)区间 为
为 .
.
【解析】
试题分析:(1) ∵ 是奇函数,,∴
是奇函数,,∴ ,∴
,∴ ,
,
∴ ;
;
(2)只需要求出 的解析式即可,利用奇函数
的解析式即可,利用奇函数 ,所以设
,所以设 ,则
,则 ,则
,则 ,再与
,再与 的解析式和在一起,写出分段函数;
的解析式和在一起,写出分段函数;
(3)本题是已知函数的值域求定义域问题,根据函数图象可得 在
在 上单调递增,分别讨论
上单调递增,分别讨论 ,
, 来求解,当
来求解,当 时,
时, 解得
解得 ;当
;当 时,
时, 解得
解得 ;所以区间
;所以区间 为
为 .
.
试题解析:(1)∵ 是奇函数,
是奇函数,
∴ 3分
3分
(2)设 ,则
,则 ,∴
,∴
∵ 为奇函数,∴
为奇函数,∴ 5分
5分
∴ 6分
6分
(3)根据函数图象可得 在
在 上单调递增 7分
上单调递增 7分
当 时,
时, 解得
解得 9分
9分
当 时,
时, 解得
解得 11分
11分
∴区间 为
为 . 12分
. 12分
考点:本题考查函数的性质(奇函数);函数的解析式;函数的定义域和值域.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目