题目内容

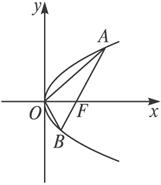
F为抛物线y2=2px(p＞0)的焦点,过F作直线交抛物线于A、B两点,记△AOB的面积为S,线段AB的长为l,试证为定值.

证明:设过焦点的直线与抛物线交于A(x1,y1)、B(x2,y2).

(1)若AB不与x轴垂直,则可设AB的方程为y=k(x-)(k≠0).

由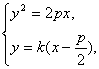得k2x2-p(k2+2)x+=0,

∴x1+x2=.

又|AF|=x1+,|BF|=x2+,

∴l=|AB|=x1+x2+p=.

设O到AB的距离为d,d=,

∴(定值).

(2)若AB与x轴垂直,则l=2p,d=,

∴(定值).


练习册系列答案
相关题目
已知点M是抛物线y2=2px（p＞0）位于第一象限部分上的一点，且点M与焦点F的距离|MF|=2p，则点M的坐标为（　　）
A、（
3p
2
，
3
p）
B、（
3p
2
，-
3
p）
C、（
3p
2
，±
3
p）
D、（
3
p，
3p
2
）
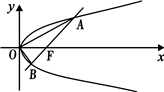精英家教网过直角坐标平面xOy中的抛物线y2=2px（p＞0）的焦点F作一条倾斜角为
π4
的直线与抛物线相交于A、B两点．
（1）求直线AB的方程；
（2）试用p表示A、B之间的距离；
（3）当p=2时，求∠AOB的余弦值．
参考公式：（xA2+yA2）（xB2+yB2）=xAxB[xAxB+2p（xA+xB）+4p2]．
已知抛物线y2=2px（p＞0）的焦点为F，准线为l．
（1）求抛物线上任意一点Q到定点N（2p，0）的最近距离；
（2）过点F作一直线与抛物线相交于A，B两点，并在准线l上任取一点M，当M不在x轴上时，证明：
kMA+kMBkMF
是一个定值，并求出这个值．（其中kMA，kMB，kMF分别表示直线MA，MB，MF的斜率）
（2012•房山区一模）F是抛物线y2=2px（p＞0）的焦点，过焦点F且倾斜角为θ的直线交抛物线于A，B两点，设|AF|=a，|BF|=b，则：
①若θ=60°且a＞b，则
a
b
的值为
3
3
；②a+b=
|AB|=
2p
sin2θ
或
2p(tan2θ+1)
tan2θ
|AB|=
2p
sin2θ
或
2p(tan2θ+1)
tan2θ
（用p和θ表示）．
（2012•温州二模）抛物线y2=2px（p＞0）的焦点为F，其准线经过双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左顶点，点M为这两条曲线的一个交点，且|MF|=2p，则双曲线的离心率为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网