题目内容
 函数
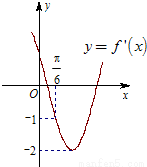
函数 的导函数y=f′(x)的图象如图所示,则m=________.
的导函数y=f′(x)的图象如图所示,则m=________.
-1
分析:先对函数f(x)求导,再由导函数的图象可知:对称轴为x=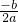 <0,图象经过原点,据此可求得m的值.
<0,图象经过原点,据此可求得m的值.
解答:∵f′(x)=x2-2mx+m2-1,而由导函数y=f′(x)的图象可知:对称轴x=m<0,图象经过原点,
∴ ,
,
解得m=-1.
故答案是-1.
点评:本题考查利用导函数的图象求参数,正确求导和利用图象提供的信息是解决问题的关键.
分析:先对函数f(x)求导,再由导函数的图象可知:对称轴为x=
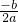 <0,图象经过原点,据此可求得m的值.
<0,图象经过原点,据此可求得m的值.解答:∵f′(x)=x2-2mx+m2-1,而由导函数y=f′(x)的图象可知:对称轴x=m<0,图象经过原点,
∴
 ,
,解得m=-1.
故答案是-1.
点评:本题考查利用导函数的图象求参数,正确求导和利用图象提供的信息是解决问题的关键.

练习册系列答案
相关题目
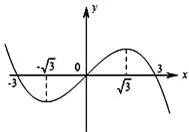 设三次函数f(x)的导函数为f′(x),函数y=x•f′(x)的图象的一部分如图所示,则正确的是( )
设三次函数f(x)的导函数为f′(x),函数y=x•f′(x)的图象的一部分如图所示,则正确的是( )A、f(x)的极大值为f(
| ||||
B、f(x)的极大值为f(-
| ||||
| C、f(x)的极大值为f(-3),极小值为f(3) | ||||
| D、f(x)的极大值为f(3),极小值为f(-3) |
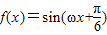 的导函数y=f'(x)的部分图象如图所示:图象与y轴交点
的导函数y=f'(x)的部分图象如图所示:图象与y轴交点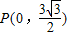 ,与x轴正半轴的交点为A、C,B为图象的最低点,则函数y=f'(x)在点C处的切线方程为 .
,与x轴正半轴的交点为A、C,B为图象的最低点,则函数y=f'(x)在点C处的切线方程为 .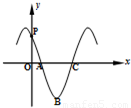
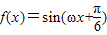 的导函数y=f'(x)的部分图象如图所示:图象与y轴交点
的导函数y=f'(x)的部分图象如图所示:图象与y轴交点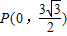 ,与x轴正半轴的交点为A、C,B为图象的最低点,则函数y=f'(x)在点C处的切线方程为 .
,与x轴正半轴的交点为A、C,B为图象的最低点,则函数y=f'(x)在点C处的切线方程为 .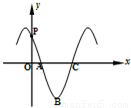
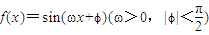 的导函数y=f'(x)的部分图象如图所示,且导函数f'(x)有最小值-2,则ω= ,ϕ= .
的导函数y=f'(x)的部分图象如图所示,且导函数f'(x)有最小值-2,则ω= ,ϕ= .