题目内容
公差d≠0的等差数列{an}的前n项和为Sn，已知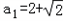
，
．
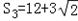（1）求数列{an}的通项公式an及其前n项和Sn；
（2）记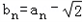
，若自然数η1，η2，…，ηk，…满足1≤η1＜η2＜…＜ηk＜…，并且
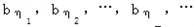成等比数列，其中η1=1，η2=3，求ηk（用k表示）；
（3）记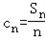
，试问：在数列{cn}中是否存在三项cr，cs，ct（r＜s＜t，r，s，t∈N*）恰好成等比数列？若存在，求出此三项；若不存在，请说明理由．
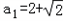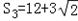，．（1）求数列{an}的通项公式an及其前n项和Sn；
（2）记
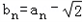，若自然数η1，η2，…，ηk，…满足1≤η1＜η2＜…＜ηk＜…，并且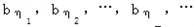成等比数列，其中η1=1，η2=3，求ηk（用k表示）；（3）记
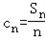，试问：在数列{cn}中是否存在三项cr，cs，ct（r＜s＜t，r，s，t∈N*）恰好成等比数列？若存在，求出此三项；若不存在，请说明理由．解：（1）∵
，
，
∴d=2
所以
，
（2）由题意，bn=2n，首项b1=2，
又数列
的公比
∴
，
又
，
∴ηk=3 k﹣1
（3）易知
，假设存在三项cr，cs，ct成等比数列，则
cs2=cr
ct，
即
，
整理得
①当2s﹣r﹣t≠0时，
，
∵r，s，t∈N*，
∴
是有理数，
这与
为无理数矛盾
②当2s﹣r﹣t=0时，则rt+r+t﹣s2﹣2s=0，从而
，
解得r=t，这与r＜t矛盾．
综上所述，不存在满足题意的三项cr，cs，ct
，，∴d=2
所以
，（2）由题意，bn=2n，首项b1=2，
又数列
的公比∴
，又
，∴ηk=3 k﹣1
（3）易知
，假设存在三项cr，cs，ct成等比数列，则cs2=cr
ct，即
，整理得
①当2s﹣r﹣t≠0时，
，∵r，s，t∈N*，
∴
是有理数，这与
为无理数矛盾②当2s﹣r﹣t=0时，则rt+r+t﹣s2﹣2s=0，从而
，解得r=t，这与r＜t矛盾．
综上所述，不存在满足题意的三项cr，cs，ct
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目