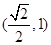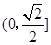题目内容
已知点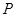 是椭圆
是椭圆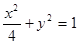 上的在第一象限内的点,又
上的在第一象限内的点,又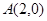 、
、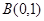 ,
,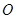 是原点,则四边形
是原点,则四边形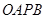 的面积的最大值是 。
的面积的最大值是 。
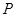 是椭圆
是椭圆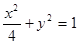 上的在第一象限内的点,又
上的在第一象限内的点,又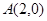 、
、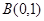 ,
,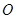 是原点,则四边形
是原点,则四边形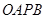 的面积的最大值是 。
的面积的最大值是 。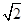
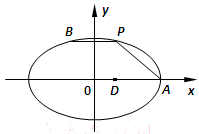
解:由于点P是椭圆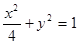 上的在第一象限内的点,
上的在第一象限内的点,
设P为(2cosa,sina)即x=2cosa, y="sina" (0<a<π),
这样四边形OAPB的面积就可以表示为两个三角形OAP和OPB面积之和,
对于三角形OAP有面积S1="sina" 对于三角形OBP有面积S2=cosa∴四边形的面积S=S1+S2=sina+cosa
=" 2" sin(a+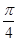 )
)
其最大值就应该为 2 ,
并且当且仅当a=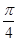 时成立.所以,面积最大值
时成立.所以,面积最大值 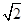 .
.
故答案为: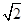 .
.
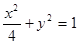 上的在第一象限内的点,
上的在第一象限内的点,设P为(2cosa,sina)即x=2cosa, y="sina" (0<a<π),
这样四边形OAPB的面积就可以表示为两个三角形OAP和OPB面积之和,
对于三角形OAP有面积S1="sina" 对于三角形OBP有面积S2=cosa∴四边形的面积S=S1+S2=sina+cosa
=" 2" sin(a+
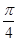 )
)其最大值就应该为 2 ,
并且当且仅当a=
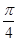 时成立.所以,面积最大值
时成立.所以,面积最大值 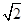 .
.故答案为:
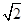 .
.
练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
 :
: ,a,b为常数),动圆
,a,b为常数),动圆 ,
, 。点
。点 分别为
分别为 与
与 与直线
与直线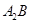 交点M的轨迹方程;
交点M的轨迹方程; 与
与 四点,其中
四点,其中 ,
, 。若矩形
。若矩形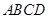 与矩形
与矩形 的面积相等,证明:
的面积相等,证明: 为定值。
为定值。

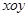 中,已知点
中,已知点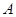 为椭圆
为椭圆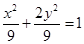 的右顶点, 点
的右顶点, 点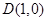 ,点
,点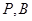 在椭
在椭 .
.
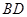 的方程;
的方程;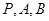 三点的圆
三点的圆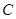 截得的弦长;
截得的弦长;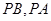 为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不存在,请说明理由.
为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不存在,请说明理由.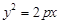 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )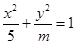 的离心率
的离心率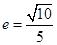 ,则
,则 的值为 ( ).
的值为 ( ). 
 或
或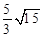
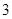 或
或
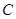 与椭圆
与椭圆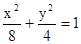 有相同的焦点,直线
有相同的焦点,直线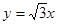 为
为 倍后得到点Q(x,
倍后得到点Q(x, ·
· ="1."
="1."  的直线L交曲线C于M、N两点,且
的直线L交曲线C于M、N两点,且 +
+ +
+ =
= ,试求△MNH的面积.
,试求△MNH的面积. 分别为椭圆
分别为椭圆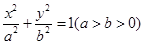 的左、右顶点,若在椭圆上存在异于
的左、右顶点,若在椭圆上存在异于 ,使得
,使得 ,其中
,其中 为坐标原点,则椭圆的离心率
为坐标原点,则椭圆的离心率 的取值范围是
的取值范围是