题目内容
已知函数 ,
,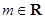 .
.
(1)若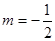 ,求证:函数
,求证:函数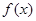 是
是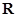 上的奇函数;
上的奇函数;
(2)若函数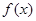 在区间
在区间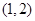 上没有零点,求实数
上没有零点,求实数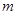 的取值范围.
的取值范围.
 ,
,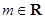 .
.(1)若
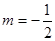 ,求证:函数
,求证:函数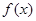 是
是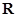 上的奇函数;
上的奇函数;(2)若函数
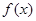 在区间
在区间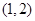 上没有零点,求实数
上没有零点,求实数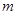 的取值范围.
的取值范围.(1)详见解析;(2)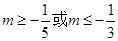 .
.
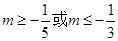 .
.试题分析:(1)定义域关于原点对称,将
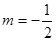 代入算得
代入算得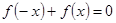
(2)考虑用补集思想解决此问题,因为
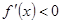 ,所以函数
,所以函数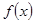 为单调递减函数,如果有零点,则
为单调递减函数,如果有零点,则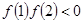 ,得到
,得到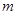 的取值范围,因为是求没有零点的
的取值范围,因为是求没有零点的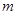 的取值范围,所以再求其补集.
的取值范围,所以再求其补集.试题解析:解:(1 )定义域为
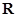 关于原点对称.
关于原点对称.因为
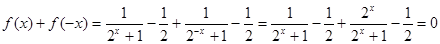 ,
,所以函数
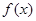 是定义在
是定义在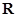 上的奇函数
上的奇函数(2)
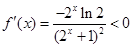
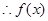 是实数集
是实数集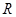 上的单调递减函数(不说明单调性扣2分)又函数
上的单调递减函数(不说明单调性扣2分)又函数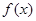 的图象不间断,在区间
的图象不间断,在区间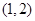 恰有一个零点,有
恰有一个零点,有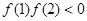
即
 解之得
解之得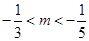 ,故函数
,故函数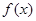 在区间
在区间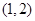 没有零点时,实数
没有零点时,实数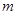 的取值范围是
的取值范围是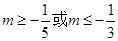 14分
14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
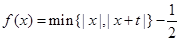 恰有三个零点,则t的值为( ).
恰有三个零点,则t的值为( ).
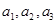 均为正数,
均为正数,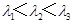 ,则函数
,则函数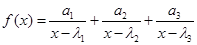 的两个零点分别位于区间( )
的两个零点分别位于区间( )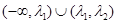 内
内 内
内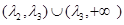 内
内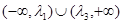 内
内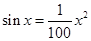 的正实根个数为( )
的正实根个数为( ) 设f(x)=(2x-1)?(x-1),且关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,则x1、x2、x3的取值范围是________.
设f(x)=(2x-1)?(x-1),且关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,则x1、x2、x3的取值范围是________. 则下列关于y=f[f(x)]-2的零点个数判断正确( ).
则下列关于y=f[f(x)]-2的零点个数判断正确( ).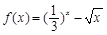 的零点所在区间为( )
的零点所在区间为( )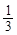 )
)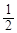 )
)