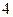题目内容
已知等比数列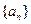 的前
的前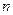 项和为
项和为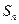 ,且点
,且点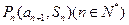 在函数
在函数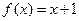 的图象上.
的图象上.
(1)求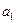 的值;
的值;
(2)若数列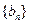 满足:
满足: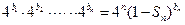 ,且
,且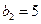 .求数列
.求数列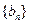 的通项公式.
的通项公式.
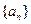 的前
的前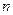 项和为
项和为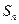 ,且点
,且点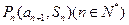 在函数
在函数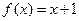 的图象上.
的图象上.(1)求
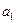 的值;
的值;(2)若数列
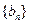 满足:
满足: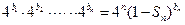 ,且
,且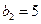 .求数列
.求数列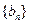 的通项公式.
的通项公式.(1)
(2)

(2)

(1)因为点 在函数
在函数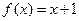 的图象上,所以
的图象上,所以 ,因为
,因为 ,
, ,
, ,
, .又数列
.又数列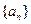 为等比数列,所以
为等比数列,所以 ,即
,即 ,故
,故 ,或
,或 (舍去).
(舍去).
(2)由(1)知数列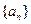 是以
是以 为首项,
为首项, 为公比的等比数列.所以
为公比的等比数列.所以
 ,
, .由
.由
 ,得
,得 对
对 成立. ①
成立. ①
则 对
对 成立. ②
成立. ②
②-①,得 ,即
,即 对
对 成立. ③
成立. ③
则有 对
对 成立. ④
成立. ④
④-③,得 ,
, ,即
,即 对
对 成立.由等差数列定义,知
成立.由等差数列定义,知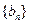 为等差数列.当
为等差数列.当 时,由①式得
时,由①式得 ,
, ,则公差
,则公差 ,所以
,所以 .
.
 在函数
在函数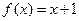 的图象上,所以
的图象上,所以 ,因为
,因为 ,
, ,
, ,
, .又数列
.又数列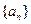 为等比数列,所以
为等比数列,所以 ,即
,即 ,故
,故 ,或
,或 (舍去).
(舍去).(2)由(1)知数列
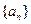 是以
是以 为首项,
为首项, 为公比的等比数列.所以
为公比的等比数列.所以
 ,
, .由
.由
 ,得
,得 对
对 成立. ①
成立. ①则
 对
对 成立. ②
成立. ②②-①,得
 ,即
,即 对
对 成立. ③
成立. ③则有
 对
对 成立. ④
成立. ④ ④-③,得
 ,
, ,即
,即 对
对 成立.由等差数列定义,知
成立.由等差数列定义,知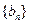 为等差数列.当
为等差数列.当 时,由①式得
时,由①式得 ,
, ,则公差
,则公差 ,所以
,所以 .
.
练习册系列答案
相关题目
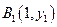 、
、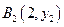 、…、
、…、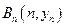 (n∈N)顺次为一次函数
(n∈N)顺次为一次函数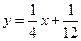 图像上的点,点列
图像上的点,点列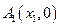 、
、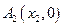 、…、
、…、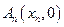 (n∈N)顺次为x轴正半轴上的点,其中
(n∈N)顺次为x轴正半轴上的点,其中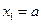 (0<a<1),对于任意n∈N,点
(0<a<1),对于任意n∈N,点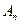 、
、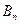 、
、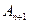 构成一个顶角的顶点为
构成一个顶角的顶点为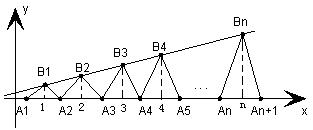
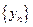 的通项公式,并证明
的通项公式,并证明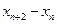 为常数,并求出数列
为常数,并求出数列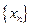 的通项公式;
的通项公式;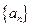 中,
中,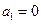 ,且对任意
,且对任意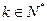 .
.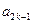 ,
,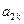 ,
,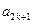 成等差数列,其公差为
成等差数列,其公差为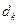 。
。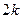 ,证明
,证明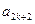 成等比数列(
成等比数列(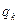 。 证明:对任意
。 证明:对任意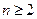 ,
,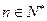 ,有
,有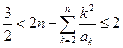
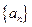 的前n项积为
的前n项积为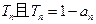 ;数列
;数列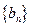 的前n项和为
的前n项和为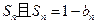 .
.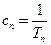 .①证明数列
.①证明数列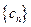 成等差数列;②求证数列
成等差数列;②求证数列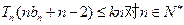 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.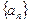 中,已知
中,已知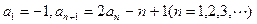
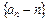 是等比数列
是等比数列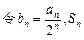 为数列
为数列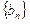 的前
的前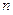 项和,求
项和,求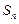 的表达式
的表达式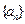 的首项
的首项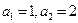 ,前
,前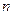 项和
项和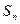 恒为正数,且当
恒为正数,且当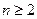 时,
时,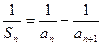 .
.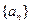 的通项公式;
的通项公式;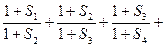
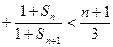 .
.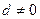 的等差数列{an}中的项组成一个新数列
的等差数列{an}中的项组成一个新数列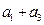 ,
, 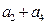 ,
,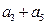 ,…,则下列说法正确的是
,…,则下列说法正确的是 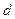 的等差数列
的等差数列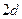 的等差数列
的等差数列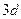 的等差数列
的等差数列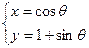 的中心到直线y=kx的距离记为d=f(k)给出下列判断
的中心到直线y=kx的距离记为d=f(k)给出下列判断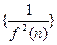 的前n项和是
的前n项和是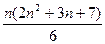
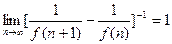 ④
④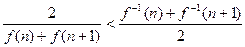
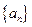 中,
中,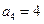 ,则
,则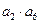 等于--------------------------------( )
等于--------------------------------( )